最強 AI 投資分析:打造自己的股市顧問機器人,股票趨勢分析×年報解讀×選股推薦×風險管理
投資個股的總風險可分成: 系統性風險(systematic risk) 與 非系統性風險 (unsystematic risk)
Blog: 系統性風險全面解析:與非系統性風險有何不同?投資者必讀!
簡單來說,系統性風險 是指影響整個市場的風險因素,它不僅僅影響某一支股票或某個產業,而是會波及整個經濟體系。
這種風險通常來自於大規模的經濟、政治或社會事件,對市場造成普遍性的影響。
假設你投資了台灣的半導體產業,如果台積電因為內部管理問題導致股價下跌,這就是一個非系統性風險的例子。它主要影響台積電及其相關的供應鏈公司,但不會對整個台灣股市造成普遍性影響。其他行業如金融業或傳統製造業,可能不會受到明顯影響。
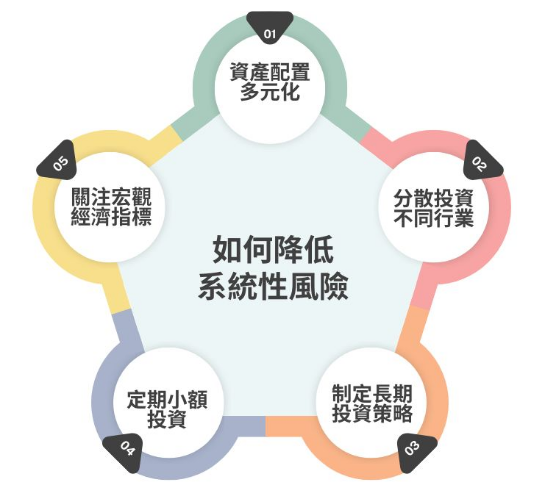
- 如何降低系統性風險?
資本資產定價模型(Capital Asset Pricing Model, CAPM)是由 William Sharpe, John Lintner, Jack Treynor 等人以馬克維茲現代投資組合理論為基礎發展出來的模型,表示了資產的預期風險與預期報酬率之間線性關係,簡化了過去投資組合運算過程,成為現在投資理財的基礎
ra = rf + βa * ( rm – rf )
-
ra:投資組合 / 單一資產的期望報酬率
-
rf ( risk free rate ):無風險資產的報酬率,通常都用 10 年期的美國政府債券為代表
-
rm ( expected market rate ):市場期望報酬率,或是已充分分散風險的投資組合期望報酬率
-
rm – rf:股票市場溢價,或是投資人要求的風險貼水,也就是相較無風險利率多賺的部分
-
βa ( beta ):單一資產 / 投資組合的系統性風險係數,顯示相對總體市場的波動性
股利折現模型認為,股票價格只是市場供需關係的表現,不一定能反映出股票的真正價值,股票的價值應該取決於公司持續經營的狀況,而這個可以由公司逐年發放的股利看出,因為股利發放多寡與公司的經營業績有關,這是公司的正現金流,所以股東權益的當前價值,會等於其未來所獲得的股利現值之和。
股價=明年股利 ÷(預期報酬率-股利成長率)
P = D/(R – G)
其中P為股價、D為現金股利、R為(高登)預期報酬率、G為股利成長率(保留盈餘成長率)。
R = D / P + G
投資者的投資期內總回報(Total Return)可分成兩部分,一部分是投資者獲得的股息收入(Income),另一部分則是股價上升帶來的回報,即是資本的增值(Capital Gain)。
前景理論(prospect theory)
其中,包含人對於決策後的預期心理,倘若有更高的利益報酬,多數人會小心評估冒更大風險的代價,但若某項決策,則會造成利益損失,則人們傾向冒更大的風險,追求更好的利益。
前景理論(Prospect theory)正也呼應心理學家Barry Schwartz認為人面對選擇有兩種思考類型:
第一、適可而止型(satisfier)。不要求十全十美,只要還不錯滿意,不是最差的就可以了。
第二、錙銖必較型(maximizer)。務必要得到最佳選擇,比較每一種的可能性,算出每種的CP值
定錨效應(Anchoring Effect)
錨定效應指的是接觸新事物的第一印象,將影響後續的判斷。
要避免做出偏誤的決策,廣納他人意見是可考慮的方式。
心理帳戶(Mental Accounting)
心理帳戶(Mental Accounting)是一種行為經濟學理論,主要描述人們如何將個人經濟活動劃分為不同的帳戶或“桶”,並根据這些劃分來進行消費和投資決策。這種理論由理查德·塞勒(Richard Thaler)提出,他認為人們在處理金錢時,會根據金錢的來源和預期用途將其分配到不同的心理帳戶中。
這種心理帳戶會受三個主要特點影響:
1、源頭效應: 人們會根據金錢的來源,如工資、獎金、禮物等,將其劃分到不同的帳戶。
2、指定效應: 人們會根據資金的預期用途,如日常開銷、旅遊、教育等,進行分類。
3、交易成本: 不同帳戶的金錢在交換和使用時被認為有不同的價值和交易成本。
- Documentations
pip install openai - API reference
Gemini API Key
Gemini 模型
實驗版模型
Gemini 2.0 Flash Thinking 模型是一種實驗模型,經過訓練後,可產生模型在回應過程中經歷的「思考過程」。因此,Flash Thinking 模型的回覆比 Gemini 2.0 Flash 實驗模型更能發揮推理能力。
進入證交所網址:https://www.twse.com.tw/zh/index.html
使用開發者模式取得請求資料網址
- 取得個股日成交資訊
- 取得連續月份資料(以個股本益比為例)
- 取得當日股價
- 取得季報表資訊
- 用 requests 取得股票新聞
- 使用 Selenium 取得股票新聞 (無法執行)
- 使用 yfinance 下載股市資料
- 取得公司基本資料
- 取得損益表
- 取得法人持股比例
- 輸入 FinMind API 和帳號密碼
- 取得股價資料
- 取得損益表資料
- 取得法人買賣資料
- 使用 FinLab 下載股市資料
- 取得收盤價
- 選擇產業
- 取得財報資料
- 取得法人資料
- 開SQLite3
- 設定資料庫結構
- 傳入資料到資料庫
- 查詢表格資料
- 計算移動平均線(MA)
- 計算 MACD
- 計算 RSI
- 計算布林通道
- 能量潮指標 (On-Balance Volumem, OBV)
- 將日頻資料轉換成月頻資料
- 加入成交量
- 加入技術指標
- 繪製 K 線圖:mplfinance
- 選擇資料時間
- 用 mplfinance 繪製 K 線圖
- 加入繪圖設定
- 加入子圖
- 繪製互動式 K 線圖
- 移除非交易日空值
- 加入懸停十字軸
- 加入技術指標
- 寫成函式
- 執行函式
plotly_stock("2317", start='2022-01-01', end= None, indicator='布林通道及MACD')
ch05_stock_backtesting_gemini.ipynb
回測也稱為回溯測試,是指用歷史數據測試某種交易策略的過去表現,觀察如果時間回溯到過去執行同樣的策略,會產生什麼結果,藉此評估一個策略在未來是否可行,以及提前了解可能的風險。
如果回測後發現,一個策略在過去按照一樣的方法執行,得到的成果很好,那也許它有機會繼續在未來創造好的表現 (但並非絕對)。
而一個策略,回測發現它在過去表現得很差,代表存在某些缺陷,我們就不會採用這個策略,因為對它未來的表現不會有信心。
回測是把自己想的交易方法,透過歷史數據進行測試,藉由查看回測結果(過去表現),了解一個交易方法的可行性和有效性。
理論上,一個未來能賺錢的投資策略,至少要在過去也能賺錢,回測就是驗證的方式。
策略經過歷史模擬,更能歷久不衰,獲取超額報酬!
FinLab 提供台股 Python 量化交易最前瞻的技術、資料庫、演算法,幫助您開發選股策略,獲取超額報酬:
- 完整的股價、營收、籌碼、財報資料庫
- 超多範例,快速程式碼開發策略
- 策略儀表版
stats = ai_backtest(stock_id="2330.TW",
period="5y",
user_msg="MACD",
add_msg="請設置10%的停損點與20%的停利點")
reply = backtest_analysis(stats)
print(reply)
# 策略1:MACD+停利停損
stats1 = ai_backtest(stock_id="2330.TW", period="5y",
user_msg="MACD",
add_msg="請設置10%的停損點與20%的停利點")
# 策略2:SMA
stats2 = ai_backtest(stock_id="2330.TW", period="5y",
user_msg="SMA",
add_msg="無")
# 策略3:RSI+停利停損
stats3 = ai_backtest(stock_id="2330.TW", period="5y",
user_msg="RSI",
add_msg="請設置10%的停損點與20%的停利點")
reply = backtest_analysis(stats1, stats2, stats3)
print(reply)
- 取得股價資料
- 取得基本面資料
- 取得新聞資料
- 爬取股號、股名對照表
- 取得股票名稱
- 建構 ChatGPT 模型
- 大盤趨勢報告
- 個股分析報告
- 雞蛋水餃股也能做分析
- 建立函式-取得年報
- 年報問答RAG
- 年報總結與分析
- 下載資料庫
- 檢視資料表格式
- AI 自動化選股機器人
- 趨勢報告推薦系統 : 取得個股分析報告,
- 推薦出一檔股票
- 推薦股票的評分排序
- AI 年報分析推薦系統
- 多檔股票的年報分析報告
- 根據分析結果推薦出一檔股票
- 年報分析報告評分排序
- 單次賭局的期望資產
- 單一賭局的隨機結果
- 重複賭局的資產變化
- 不同下注量的資產成長幅度
- 倍倍下注法
- 凱利公式 Kelly formula
- 取得回測結果
- 計算賠率、取得勝率及最佳下注比例
- 用凱利公式來更改策略
- 資金管理
- 設定投資組合
- 計算每月的漲幅或跌幅
- 計算每檔股票的最佳下注比例
- 比較平均分配與使用下注比例的報酬
- 與大盤績效進行比較
- 投資組合標準差 (σ)
- 風險值 (Value at Risk, VaR)
- beta 係數 (β)
- 夏普比率 (Sharpe Ratio)