Solver with adaptive mesh refinement written in Python. Multiple Riemann solvers (HLLC, Flux Vector Splitting) are implemented, based on [1]. The spatial scheme can be of order 1 (piecewise constant) or 2 (MUSCL-Hancock scheme with linear reconstruction). A minmod limiter is also avaible. The temporal integration is either first-order (Explicit Euler), third-order (SSP Runge-Kutta method), or any of Scip's 'solve_ivp' methods. Dynamic time step is available (either via error estimates with Scipy or via a CFL condition).
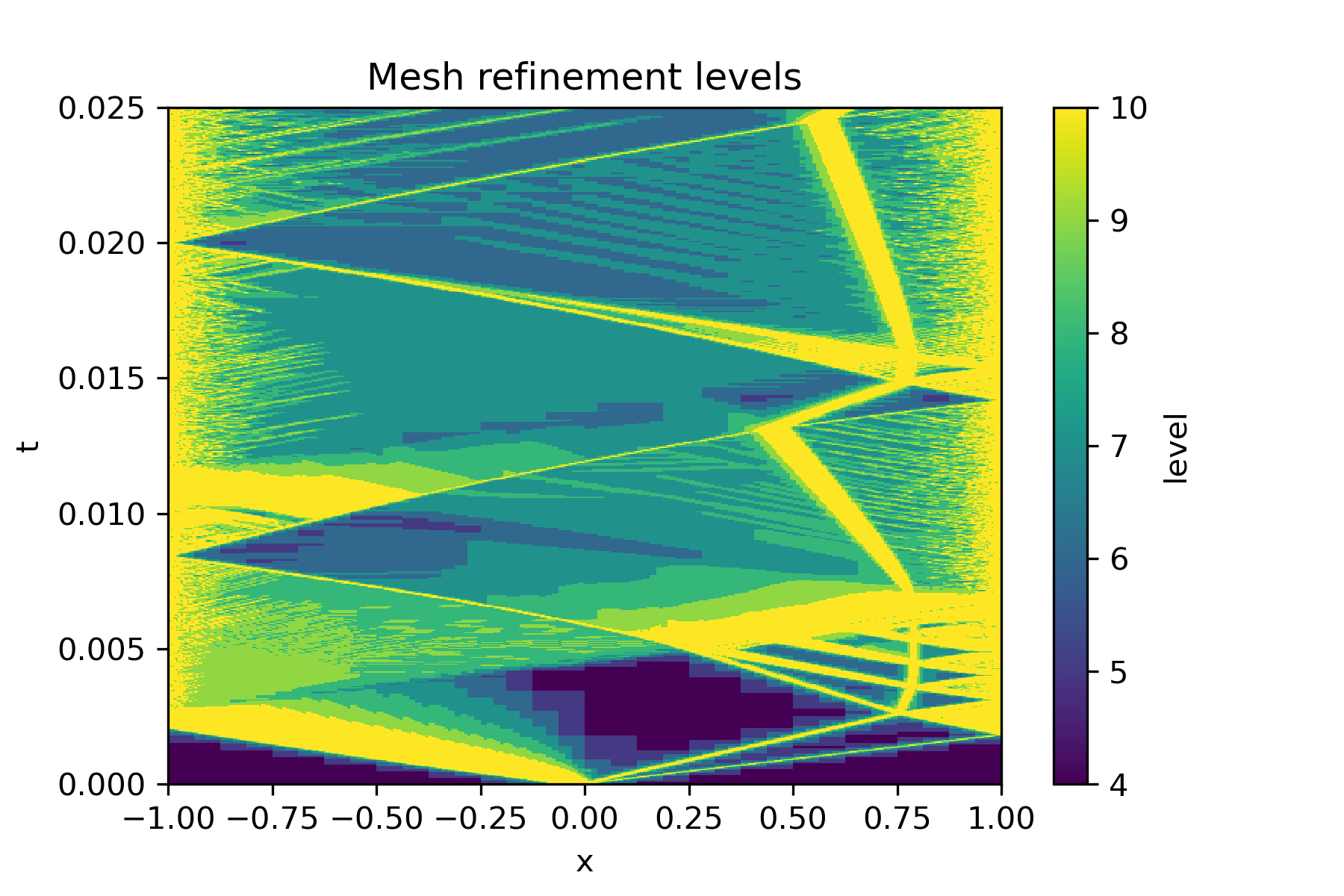
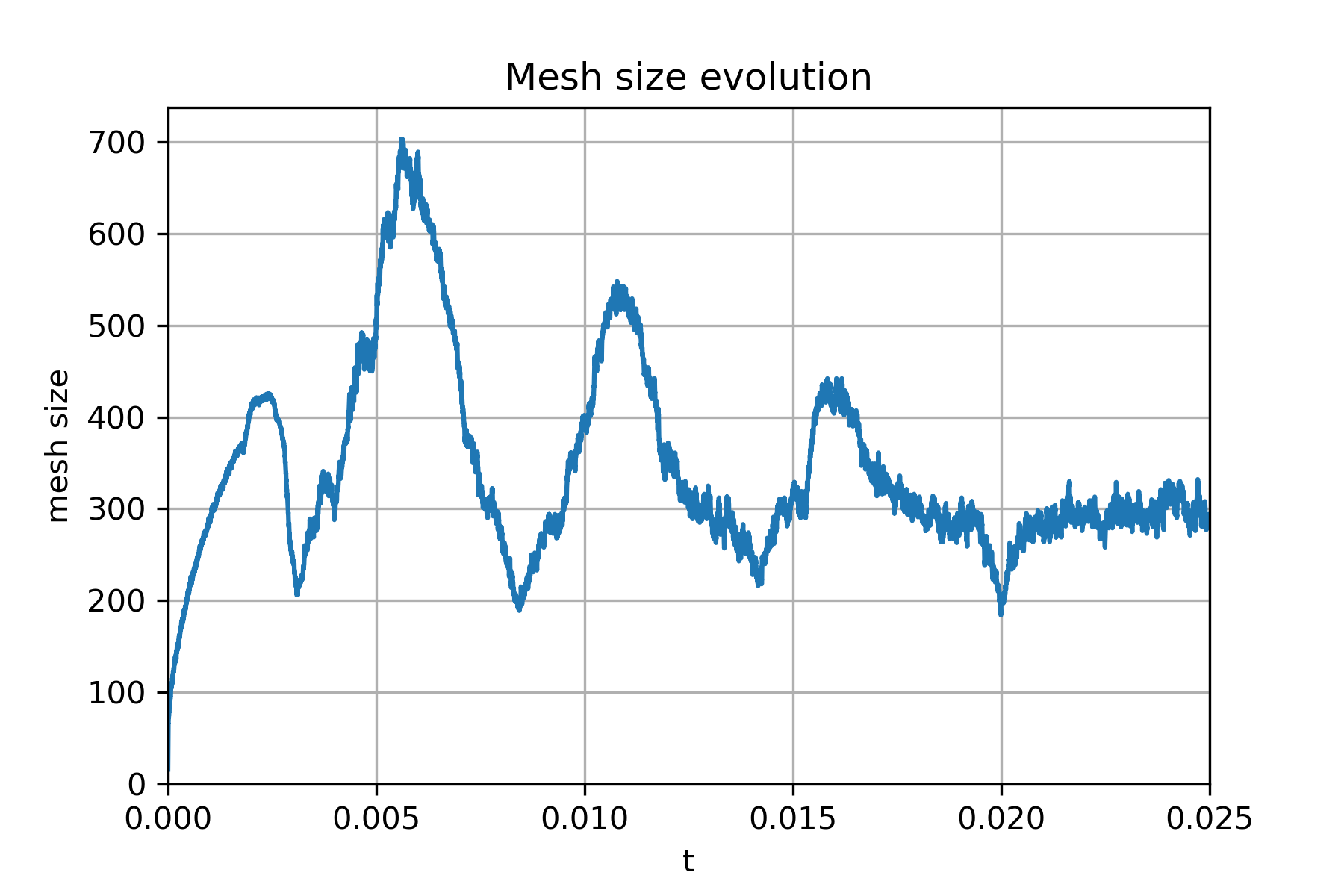
A tree-based dynamic refinement algorithm is implemented. Various refinement criteria are available: error estimate of the spatial discretisation, classical "gradient" of some variables...
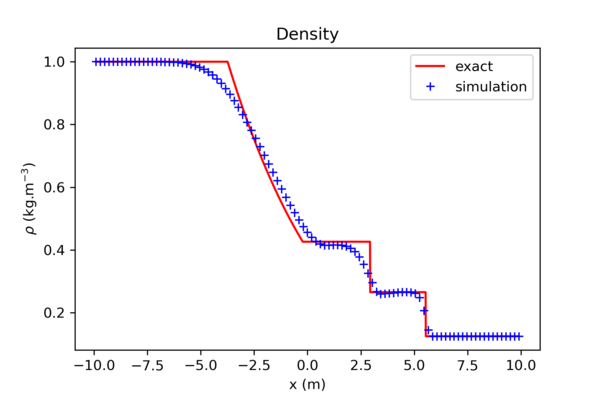
The test script implements the classical Sod shock tube problem, with reflective or transmissive boundaries.
Here is a comparison of the density field at t=0.01s, for the analytical solution and for the simulation with 100 cells, order 2 reconstruction and Flux Vector Splitting:
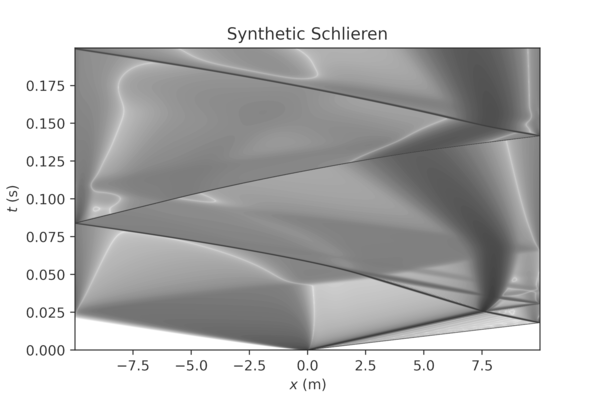
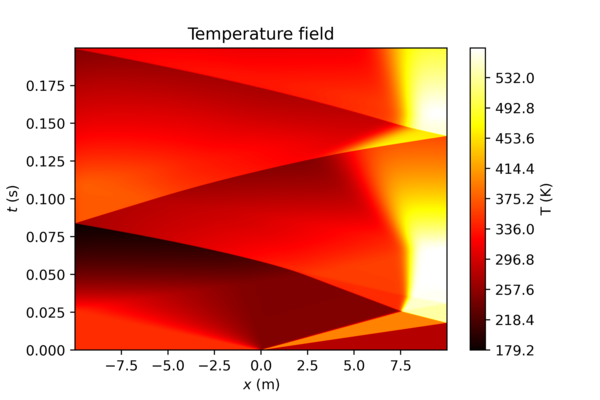
Some fancy visualizations can be obtained with this code, for example the following wave diagrams, for a shock tube with reflective boundaries (1000 uniform cells):
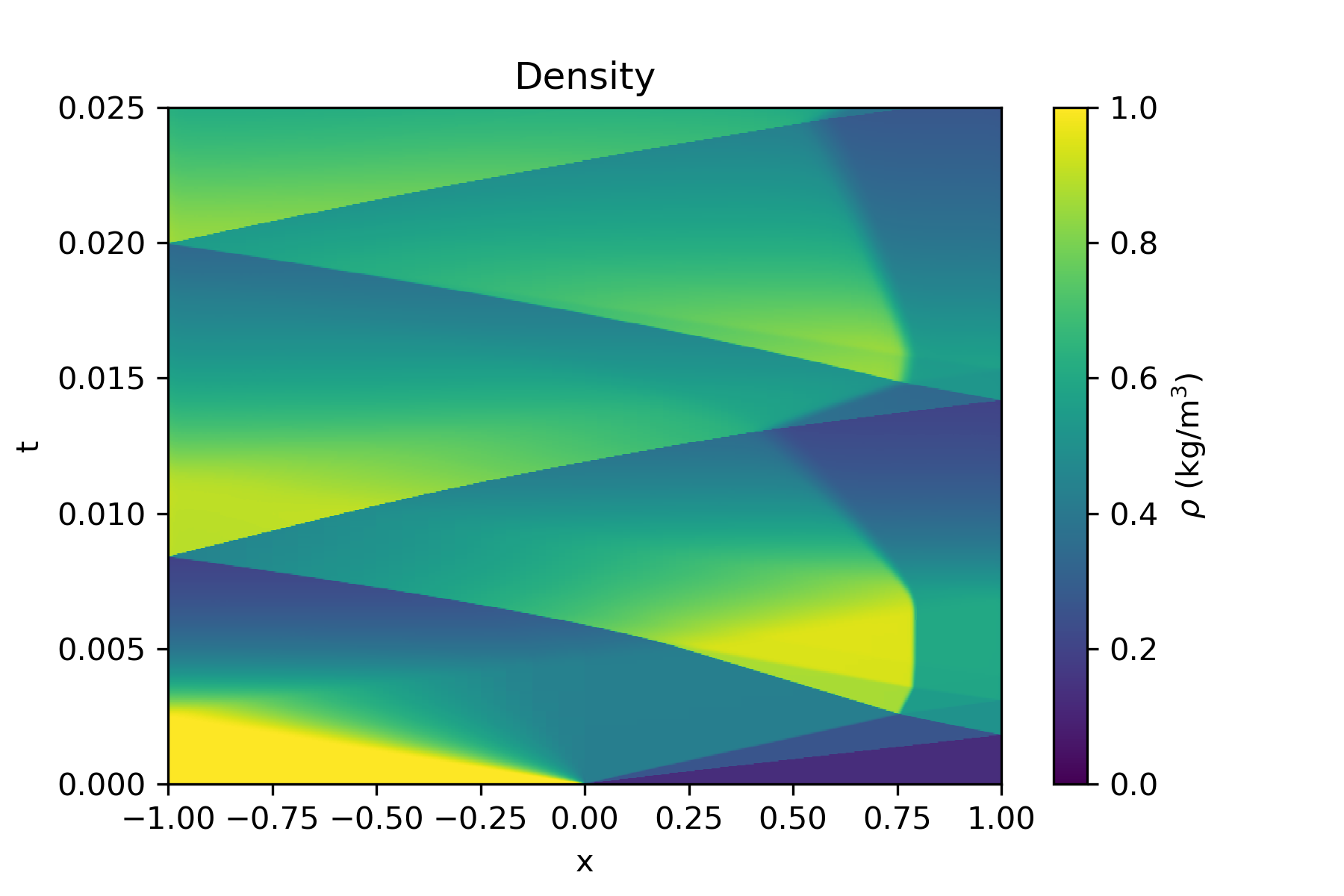
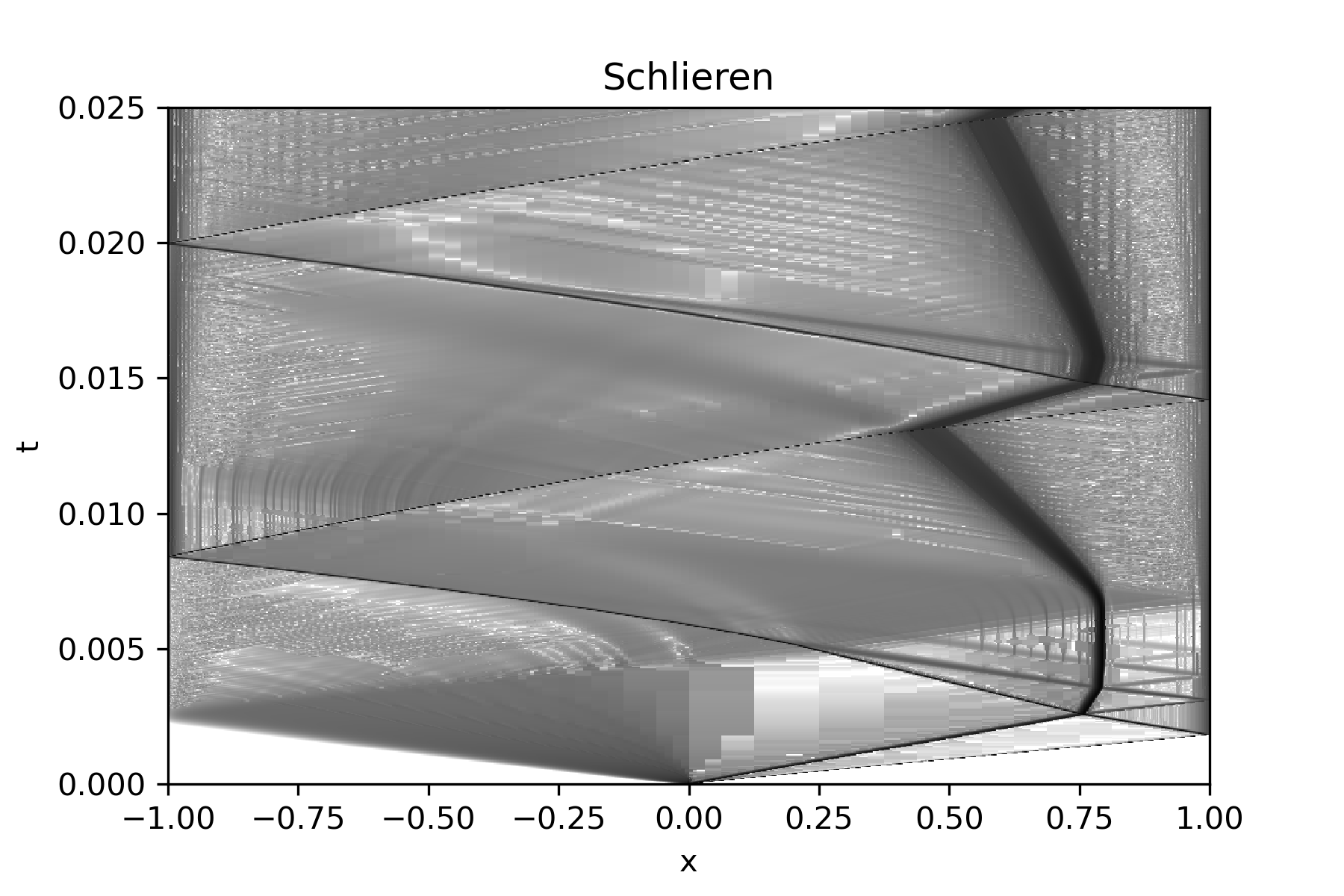
Here is a similar test case, with adaptive mesh refinement:
References: [1] "Riemann Solvers and Numerical Methods for Fluid Dynamics, A Practical Introduction" by Toro, Eleuterio F., Springer
TODO: quasi-1D version