操作系统:Windows 10 64位
编程语言:C++ 14、Python 3.8
编译器:CLion 2020.3 x64
项目目录结构如下:
├─AStarSearch.cpp ------ // A*算法类实现
├─AStarSearch.h -------- // A*算法类定义
├─CMakeLists.txt ------- // 编译文件
├─generator.py --------- // 用例生成脚本
├─Node.cpp ------------- // 节点类实现
├─Node.h --------------- // 节点类定义
├─npuzzle.cpp ---------- // 主程序
├─test.cpp ------------- // 测试程序
└─Testcase ------------- // 存放测试用例
├─Inputcase ---------- // 存放用例输入文件
├─Outcome ------------ // 存放结果输出文件
└─Test_outcome ------- // 存放测试结果输出文件
特别说明:C++所有程序只能有一个main函数,所以为了避免编译报错,运行主程序或测试程序之前请在编译文件中选择相应的指令(在CMakeLists.txt中将另外一个文件编译指令注释掉即可)。
N-puzzle问题是人工智能领域使用启发式算法建模的经典问题之一。
问题描述如下:给定一个
目标是使用最少数量的移动来重新排列块,使它们井然有序。移动可以是块的水平或垂直滑动。
我们使用
这是最简单的一种启发式,即统计错误放置的块的数目。这一启发式和汉明距离的概念相似。
汉明距离是使用在数据传输差错控制编码里面的,汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,我们以
这是书上介绍的第二种启发式,即对每个块到它目标位置的曼哈顿距离进行求和。
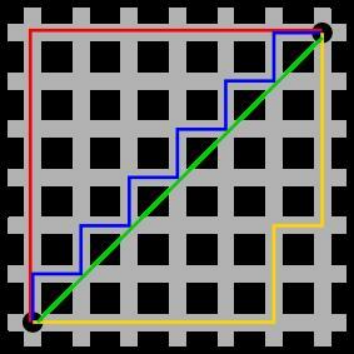
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即
$$
d(i,j)=|x_i-x_j|+|y_i-y_j|
$$
首先给出线性冲突的定义:当两个块
对于具有大量步骤的解决方案,汉明距离启发法可能需要大量内存,甚至超过5GB。最好不要对4×4或更大尺寸的板使用汉明距离启发式算法,所以本次对比分析主要选择了 3×3 和 4×4 的有解情况。
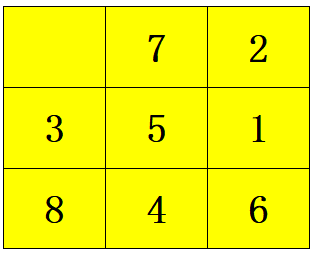
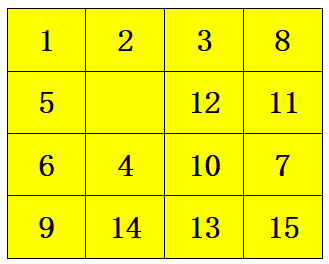
为了方便测试,在test.cpp中设计了随机生成puzzle的功能,从众多测试结果中选择了两个典型的例子进行说明。
| Heuristics | Steps | Nodes Expanded | Nodes Opened | Nodes Pushed | Max Depth Reached | Execution Time(ms) |
|---|---|---|---|---|---|---|
| MisplacedTiles (h1) | 28 | 69916 | 93175 | 93376 | 28 | 1147.58 |
| Manhattan Distance (h2) | 28 | 6617 | 10345 | 10514 | 28 | 90.02 |
| LinearConflicts (h3) | 28 | 2931 | 4642 | 4718 | 28 | 38.002 |
| Heuristics | Steps | Nodes Expanded | Nodes Opened | Nodes Pushed | Max Depth Reached | Execution Time(ms) |
|---|---|---|---|---|---|---|
| MisplacedTiles (h1) | 28 | 513013 | 989569 | 990725 | 28 | 15829.6 |
| Manhattan Distance (h2) | 28 | 13425 | 26152 | 26403 | 28 | 332.076 |
| LinearConflicts (h3) | 28 | 4495 | 8707 | 8779 | 28 | 96.035 |
通过观察上述两个典型例子及许多实验可发现:
- 随着解决步骤的增加或棋盘大小的增大,h1消耗的内存急剧增加,所需时间也最长,在许多需要较多步骤的情况下会空间溢出。h2和h3则不会出现这种情况,且二者的时间开销和空间开销比h1好得多。
- h2和h3在解决步骤较少的情况下,二者的差异并不明显。当解决步骤的增加和棋盘大小的增大时,h3所需的时间开销和空间开销会比h2小。
在程序的很多地方需要用到数组存放数据,而且无法提前预知需要的数组规模有多大,为了最大程度地节约空间,使用了C++中vector库,即容器。vector之所以被认为是一个容器,是因为它能够像容器一样存放各种类型的对象,简单地说,vector是一个能够存放任意类型的动态数组,能够增加和压缩数据。
同时对已提前预知容量的数组,仍采用动态数组分配的方式,即C++运算符new/delete。
函数传参有三种方式:传值、传地址和传引用。在设计实现时,对节点信息封装成了类,在各个操作函数传参时都使用了传引用方式,既避免函数形参拷贝增加空间开销,又能直接修改实参的值,同时引用比指针用起来相对更安全。
用来测试的puzzle例子太少且大多都是解题步骤较少的类型。针对这一问题设计了一个python脚本(generator.py)来专门生成测试用例。但每次都要先运行python脚本得到测试用例后再手动复制到读入文件,运行C++程序后才能得到结果。
为了使得测试流程更简化,用C++实现上述python脚本的功能。在test.cpp中有体现。