|
1 | | -3512\. Minimum Operations to Make Array Sum Divisible by K |
| 1 | +3515\. Shortest Path in a Weighted Tree |
2 | 2 |
|
3 | | -Easy |
| 3 | +Hard |
4 | 4 |
|
5 | | -You are given an integer array `nums` and an integer `k`. You can perform the following operation any number of times: |
| 5 | +You are given an integer `n` and an undirected, weighted tree rooted at node 1 with `n` nodes numbered from 1 to `n`. This is represented by a 2D array `edges` of length `n - 1`, where <code>edges[i] = [u<sub>i</sub>, v<sub>i</sub>, w<sub>i</sub>]</code> indicates an undirected edge from node <code>u<sub>i</sub></code> to <code>v<sub>i</sub></code> with weight <code>w<sub>i</sub></code>. |
6 | 6 |
|
7 | | -* Select an index `i` and replace `nums[i]` with `nums[i] - 1`. |
| 7 | +You are also given a 2D integer array `queries` of length `q`, where each `queries[i]` is either: |
8 | 8 |
|
9 | | -Return the **minimum** number of operations required to make the sum of the array divisible by `k`. |
| 9 | +* `[1, u, v, w']` – **Update** the weight of the edge between nodes `u` and `v` to `w'`, where `(u, v)` is guaranteed to be an edge present in `edges`. |
| 10 | +* `[2, x]` – **Compute** the **shortest** path distance from the root node 1 to node `x`. |
| 11 | + |
| 12 | +Return an integer array `answer`, where `answer[i]` is the **shortest** path distance from node 1 to `x` for the <code>i<sup>th</sup></code> query of `[2, x]`. |
10 | 13 |
|
11 | 14 | **Example 1:** |
12 | 15 |
|
13 | | -**Input:** nums = [3,9,7], k = 5 |
| 16 | +**Input:** n = 2, edges = [[1,2,7]], queries = [[2,2],[1,1,2,4],[2,2]] |
14 | 17 |
|
15 | | -**Output:** 4 |
| 18 | +**Output:** [7,4] |
16 | 19 |
|
17 | 20 | **Explanation:** |
18 | 21 |
|
19 | | -* Perform 4 operations on `nums[1] = 9`. Now, `nums = [3, 5, 7]`. |
20 | | -* The sum is 15, which is divisible by 5. |
| 22 | +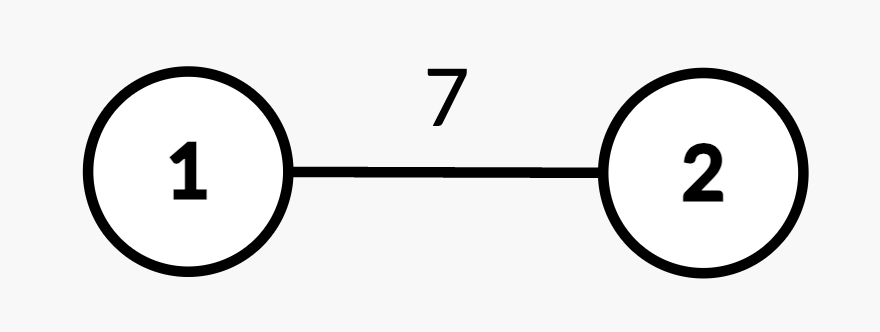 |
| 23 | + |
| 24 | +* Query `[2,2]`: The shortest path from root node 1 to node 2 is 7. |
| 25 | +* Query `[1,1,2,4]`: The weight of edge `(1,2)` changes from 7 to 4. |
| 26 | +* Query `[2,2]`: The shortest path from root node 1 to node 2 is 4. |
21 | 27 |
|
22 | 28 | **Example 2:** |
23 | 29 |
|
24 | | -**Input:** nums = [4,1,3], k = 4 |
| 30 | +**Input:** n = 3, edges = [[1,2,2],[1,3,4]], queries = [[2,1],[2,3],[1,1,3,7],[2,2],[2,3]] |
25 | 31 |
|
26 | | -**Output:** 0 |
| 32 | +**Output:** [0,4,2,7] |
27 | 33 |
|
28 | 34 | **Explanation:** |
29 | 35 |
|
30 | | -* The sum is 8, which is already divisible by 4. Hence, no operations are needed. |
| 36 | +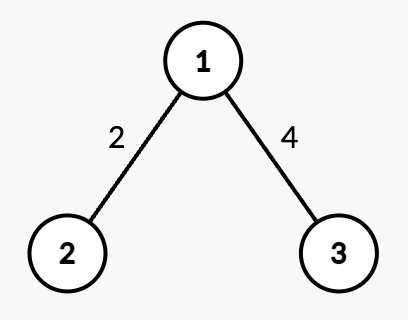 |
| 37 | + |
| 38 | +* Query `[2,1]`: The shortest path from root node 1 to node 1 is 0. |
| 39 | +* Query `[2,3]`: The shortest path from root node 1 to node 3 is 4. |
| 40 | +* Query `[1,1,3,7]`: The weight of edge `(1,3)` changes from 4 to 7. |
| 41 | +* Query `[2,2]`: The shortest path from root node 1 to node 2 is 2. |
| 42 | +* Query `[2,3]`: The shortest path from root node 1 to node 3 is 7. |
31 | 43 |
|
32 | 44 | **Example 3:** |
33 | 45 |
|
34 | | -**Input:** nums = [3,2], k = 6 |
| 46 | +**Input:** n = 4, edges = [[1,2,2],[2,3,1],[3,4,5]], queries = [[2,4],[2,3],[1,2,3,3],[2,2],[2,3]] |
35 | 47 |
|
36 | | -**Output:** 5 |
| 48 | +**Output:** [8,3,2,5] |
37 | 49 |
|
38 | 50 | **Explanation:** |
39 | 51 |
|
40 | | -* Perform 3 operations on `nums[0] = 3` and 2 operations on `nums[1] = 2`. Now, `nums = [0, 0]`. |
41 | | -* The sum is 0, which is divisible by 6. |
| 52 | +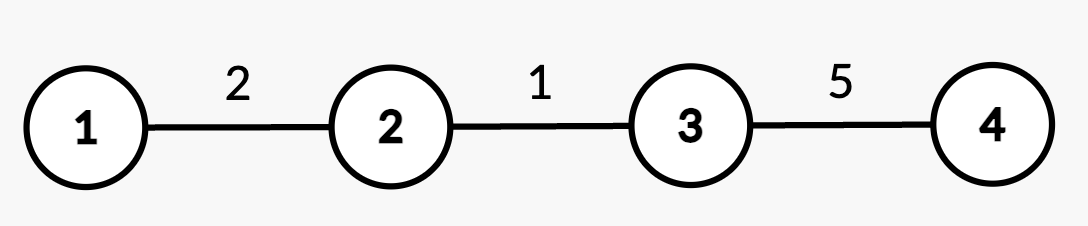 |
| 53 | + |
| 54 | +* Query `[2,4]`: The shortest path from root node 1 to node 4 consists of edges `(1,2)`, `(2,3)`, and `(3,4)` with weights `2 + 1 + 5 = 8`. |
| 55 | +* Query `[2,3]`: The shortest path from root node 1 to node 3 consists of edges `(1,2)` and `(2,3)` with weights `2 + 1 = 3`. |
| 56 | +* Query `[1,2,3,3]`: The weight of edge `(2,3)` changes from 1 to 3. |
| 57 | +* Query `[2,2]`: The shortest path from root node 1 to node 2 is 2. |
| 58 | +* Query `[2,3]`: The shortest path from root node 1 to node 3 consists of edges `(1,2)` and `(2,3)` with updated weights `2 + 3 = 5`. |
42 | 59 |
|
43 | 60 | **Constraints:** |
44 | 61 |
|
45 | | -* `1 <= nums.length <= 1000` |
46 | | -* `1 <= nums[i] <= 1000` |
47 | | -* `1 <= k <= 100` |
| 62 | +* <code>1 <= n <= 10<sup>5</sup></code> |
| 63 | +* `edges.length == n - 1` |
| 64 | +* <code>edges[i] == [u<sub>i</sub>, v<sub>i</sub>, w<sub>i</sub>]</code> |
| 65 | +* <code>1 <= u<sub>i</sub>, v<sub>i</sub> <= n</code> |
| 66 | +* <code>1 <= w<sub>i</sub> <= 10<sup>4</sup></code> |
| 67 | +* The input is generated such that `edges` represents a valid tree. |
| 68 | +* <code>1 <= queries.length == q <= 10<sup>5</sup></code> |
| 69 | +* `queries[i].length == 2` or `4` |
| 70 | + * `queries[i] == [1, u, v, w']` or, |
| 71 | + * `queries[i] == [2, x]` |
| 72 | + * `1 <= u, v, x <= n` |
| 73 | + * `(u, v)` is always an edge from `edges`. |
| 74 | + * <code>1 <= w' <= 10<sup>4</sup></code> |
0 commit comments