|
6 | 6 | [](https://coveralls.io/github/JuliaDiffEq/NeuralNetDiffEq.jl?branch=master) |
7 | 7 | [](http://codecov.io/github/JuliaDiffEq/NeuralNetDiffEq.jl?branch=master) |
8 | 8 |
|
9 | | -The repository is for the development of neural network solvers of differential equations. It is based on the work of: |
| 9 | +The repository is for the development of neural network solvers of differential equations. |
| 10 | +It utilizes techniques like neural stochastic differential equations to make it |
| 11 | +practical to solve high dimensional PDEs of the form: |
| 12 | + |
| 13 | +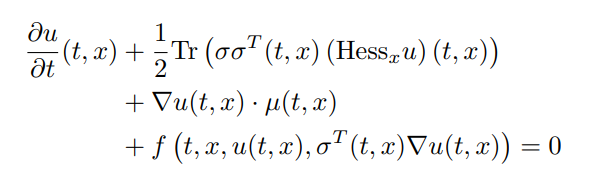 |
| 14 | + |
| 15 | +Additionally it utilizes neural networks as universal function approximators to |
| 16 | +solve ODEs. These are techniques of a field becoming known as Scientific Machine |
| 17 | +Learning (Scientific ML), encapsulated in a maintained repository. |
| 18 | + |
| 19 | +# Examples |
| 20 | + |
| 21 | +## Solving the 100 dimensional Black-Scholes-Barenblatt Equation |
| 22 | + |
| 23 | +In this example we will solve a Black-Scholes-Barenblatt equation of 100 dimensions. |
| 24 | +The Black-Scholes-Barenblatt equation is a nonlinear extension to the Black-Scholes |
| 25 | +equation which models uncertain volatility and interest rates derived from the |
| 26 | +Black-Scholes equation. This model results in a nonlinear PDE whose dimension |
| 27 | +is the number of assets in the portfolio. The PDE is of the form: |
| 28 | + |
| 29 | +![PDEFORM]() |
| 30 | + |
| 31 | +To solve it using the `TerminalPDEProblem`, we write: |
| 32 | + |
| 33 | +```julia |
| 34 | +d = 100 # number of dimensions |
| 35 | +x0 = repeat([1.0f0, 0.5f0], div(d,2)) |
| 36 | +tspan = (0.0f0,1.0f0) |
| 37 | +r = 0.05f0 |
| 38 | +sigma = 0.4f0 |
| 39 | +f(X,u,σᵀ∇u,p,t) = r * (u - sum(X.*σᵀ∇u)) |
| 40 | +g(X) = sum(X.^2) |
| 41 | +μ(X,p,t) = zero(X) #Vector d x 1 |
| 42 | +σ(X,p,t) = Diagonal(sigma*X.data) #Matrix d x d |
| 43 | +prob = TerminalPDEProblem(g, f, μ, σ, x0, tspan) |
| 44 | +``` |
| 45 | + |
| 46 | +As described in the API docs, we now need to define our `NNPDENS` algorithm |
| 47 | +by giving it the Flux.jl chains we want it to use for the neural networks. |
| 48 | +`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u` |
| 49 | +needs to be `d+1` dimensional to `d` dimensions. Thus we define the following: |
| 50 | + |
| 51 | +```julia |
| 52 | +hls = 10 + d #hide layer size |
| 53 | +opt = Flux.ADAM(0.001) |
| 54 | +u0 = Flux.Chain(Dense(d,hls,relu), |
| 55 | + Dense(hls,hls,relu), |
| 56 | + Dense(hls,1)) |
| 57 | +σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu), |
| 58 | + Dense(hls,hls,relu), |
| 59 | + Dense(hls,hls,relu), |
| 60 | + Dense(hls,d)) |
| 61 | +pdealg = NNPDENS(u0, σᵀ∇u, opt=opt) |
| 62 | +``` |
| 63 | + |
| 64 | +And now we solve the PDE. Here we say we want to solve the underlying neural |
| 65 | +SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most |
| 66 | +150 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging), |
| 67 | +and stop if the loss ever goes below `1f-6`. |
| 68 | + |
| 69 | +```julia |
| 70 | +ans = solve(prob, pdealg, verbose=true, maxiters=150, trajectories=100, |
| 71 | + alg=EM(), dt=0.2, pabstol = 1f-6) |
| 72 | +``` |
| 73 | + |
| 74 | +## Solving a 100 dimensional Hamilton-Jacobi-Bellman Equation |
| 75 | + |
| 76 | +In this example we will solve a Hamilton-Jacobi-Bellman equation of 100 dimensions. |
| 77 | +The Hamilton-Jacobi-Bellman equation is the solution to a stochastic optimal |
| 78 | +control problem. Here, we choose to solve the classical Linear Quadratic Gaussian |
| 79 | +(LQG) control problem of 100 dimensions, which is governed by the SDE |
| 80 | +`dX_t = 2sqrt(λ)c_t dt + sqrt(2)dW_t` where `c_t` is a control process. The solution |
| 81 | +to the optimal control is given by a PDE of the form: |
| 82 | + |
| 83 | +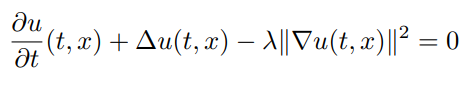 |
| 84 | + |
| 85 | +with terminating condition `g(X) = log(0.5f0 + 0.5f0*sum(X.^2))`. To solve it |
| 86 | +using the `TerminalPDEProblem`, we write: |
| 87 | + |
| 88 | +```julia |
| 89 | +d = 100 # number of dimensions |
| 90 | +x0 = fill(0.0f0,d) |
| 91 | +tspan = (0.0f0, 1.0f0) |
| 92 | +λ = 1.0f0 |
| 93 | + |
| 94 | +g(X) = log(0.5f0 + 0.5f0*sum(X.^2)) |
| 95 | +f(X,u,σᵀ∇u,p,t) = -λ*sum(σᵀ∇u.^2) |
| 96 | +μ(X,p,t) = zero(X) #Vector d x 1 λ |
| 97 | +σ(X,p,t) = Diagonal(sqrt(2.0f0)*ones(Float32,d)) #Matrix d x d |
| 98 | +prob = TerminalPDEProblem(g, f, μ, σ, x0, tspan) |
| 99 | +``` |
| 100 | + |
| 101 | +As described in the API docs, we now need to define our `NNPDENS` algorithm |
| 102 | +by giving it the Flux.jl chains we want it to use for the neural networks. |
| 103 | +`u0` needs to be a `d` dimensional -> 1 dimensional chain, while `σᵀ∇u` |
| 104 | +needs to be `d+1` dimensional to `d` dimensions. Thus we define the following: |
| 105 | + |
| 106 | +```julia |
| 107 | +hls = 10 + d #hidden layer size |
| 108 | +opt = Flux.ADAM(0.01) #optimizer |
| 109 | +#sub-neural network approximating solutions at the desired point |
| 110 | +u0 = Flux.Chain(Dense(d,hls,relu), |
| 111 | + Dense(hls,hls,relu), |
| 112 | + Dense(hls,1)) |
| 113 | +# sub-neural network approximating the spatial gradients at time point |
| 114 | +σᵀ∇u = Flux.Chain(Dense(d+1,hls,relu), |
| 115 | + Dense(hls,hls,relu), |
| 116 | + Dense(hls,hls,relu), |
| 117 | + Dense(hls,d)) |
| 118 | +pdealg = NNPDENS(u0, σᵀ∇u, opt=opt) |
| 119 | +``` |
| 120 | + |
| 121 | +And now we solve the PDE. Here we say we want to solve the underlying neural |
| 122 | +SDE using the Euler-Maruyama SDE solver with our chosen `dt=0.2`, do at most |
| 123 | +100 iterations of the optimizer, 100 SDE solves per loss evaluation (for averaging), |
| 124 | +and stop if the loss ever goes below `1f-2`. |
| 125 | + |
| 126 | +```julia |
| 127 | +@time ans = solve(prob, pdealg, verbose=true, maxiters=100, trajectories=100, |
| 128 | + alg=EM(), dt=0.2, pabstol = 1f-2) |
| 129 | + |
| 130 | +``` |
| 131 | + |
| 132 | +# API Documentation |
| 133 | + |
| 134 | +## Solving High Dimensional PDEs with Neural Networks |
| 135 | + |
| 136 | +To solve high dimensional PDEs, first one should describe the PDE in terms of |
| 137 | +the `TerminalPDEProblem` with constructor: |
| 138 | + |
| 139 | +```julia |
| 140 | +TerminalPDEProblem(g,f,μ,σ,X0,tspan,p=nothing) |
| 141 | +``` |
| 142 | + |
| 143 | +which describes the semilinear parabolic PDE of the form: |
| 144 | + |
| 145 | +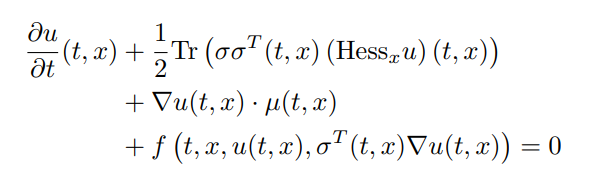 |
| 146 | + |
| 147 | +with terminating condition `u(tspan[2],x) = g(x)`. These methods solve the PDE in |
| 148 | +reverse, satisfying the terminal equation and giving a point estimate at |
| 149 | +`u(tspan[1],X0)`. The dimensionality of the PDE is determined by the choice |
| 150 | +of `X0`. |
| 151 | + |
| 152 | +To solve this PDE problem, there exists two algorithms: |
| 153 | + |
| 154 | +- `NNPDENS(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses a neural stochastic differential |
| 155 | + equation which is then solved by the methods available in DifferentialEquations.jl |
| 156 | + The `alg` keyword is required for specifying the SDE solver algorithm that |
| 157 | + will be used on the internal SDE. All of the other keyword arguments are passed |
| 158 | + to the SDE solver. |
| 159 | +- `NNPDEHan(u0,σᵀ∇u;opt=Flux.ADAM(0.1))`: Uses the stochastic RNN algorithm |
| 160 | + [from Han](https://www.pnas.org/content/115/34/8505). Only applicable when |
| 161 | + `μ` and `σ` result in a non-stiff SDE where low order non-adaptive time |
| 162 | + stepping is applicable. |
| 163 | + |
| 164 | +Here, `u0` is a Flux.jl chain with `d` dimensional input and 1 dimensional output. |
| 165 | +For `NNPDEHan`, `σᵀ∇u` is an array of `M` chains with `d` dimensional input and |
| 166 | +`d` dimensional output, where `M` is the total number of timesteps. For `NNPDENS` |
| 167 | +it is a `d+1` dimensional input (where the final value is time) and `d` dimensional |
| 168 | +output. `opt` is a Flux.jl optimizer. |
| 169 | + |
| 170 | +Each of these methods has a special keyword argument `pabstol` which specifies |
| 171 | +an absolute tolerance on the PDE's solution, and will exit early if the loss |
| 172 | +reaches this value. Its defualt value is `1f-6`. |
| 173 | + |
| 174 | +## Solving ODEs with Neural Networks |
| 175 | + |
| 176 | +For ODEs, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/latest/solvers/ode_solve.html#NeuralNetDiffEq.jl-1) |
| 177 | +for the `nnode(chain,opt=ADAM(0.1))` algorithm, which takes in a Flux.jl chain |
| 178 | +and optimizer to solve an ODE. This method is not particularly efficient, but |
| 179 | +is parallel. It is based on the work of: |
10 | 180 |
|
11 | 181 | [Lagaris, Isaac E., Aristidis Likas, and Dimitrios I. Fotiadis. "Artificial neural networks for solving ordinary and partial differential equations." IEEE Transactions on Neural Networks 9, no. 5 (1998): 987-1000.](https://arxiv.org/pdf/physics/9705023.pdf) |
0 commit comments