Improve Performance #11
Comments
|
Thanks for the write up Chris, your approach in PaddedMatrices.jl is really promising.
Absolutely. I've started a few times trying to look into your implementation in PaddedMatrices.jl and don't fully grok it yet, but I think I just need to sit down and spend more time on it. That's a nice diagram above, should be helpful. How do you forsee this going? Just making Gaius depend on PaddedMatrices and then moving (an optimized version of) the matmul code from PaddedMatrices over to Gaius, or something else? |
Here is the main function: function jmul!(C::AbstractMatrix{Tc}, A::AbstractMatrix{Ta}, B::AbstractMatrix{Tb}, ::Val{mc}, ::Val{kc}, ::Val{nc}, ::Val{log2kc}) where {Tc, Ta, Tb, mc, kc, nc, log2kc}
M, K, N = matmul_sizes(C, A, B)
Niter, Nrem = divrem(N, nc)
Miter, Mrem = divrem(M, mc)
(iszero(Miter) && iszero(Niter)) && return loopmul!(C, A, B)
Km1 = K - 1
if (1 << log2kc) == kc
Kiter = Km1 >>> log2kc
Krem = (Km1 & (kc - 1)) # Krem guaranteed to be > 0
else
Kiter, Krem = divrem(Km1, kc)
end
Krem += 1
Aptr = stridedpointer(A)
Bptr = stridedpointer(B)
Cptr = stridedpointer(C)
GC.@preserve C A B LCACHE begin
for no in 0:Niter-1
# Krem
# pack kc x nc block of B
Bpacked_krem = pack_B_krem(Bptr, Val{kc}(), Val{nc}(), Tb, Krem, no)
# Bpacked_krem = PtrMatrix{-1,nc}(gesp(Bptr, (Kiter*kc, no*nc)), Krem)
for mo in 0:Miter-1
# pack mc x kc block of A
Apacked_krem = pack_A_krem(Aptr, Val{mc}(), Ta, mo, Krem)
Cpmat = PtrMatrix{mc,nc}(gesp(Cptr, (mo*mc, no*nc)))
loopmul!(Cpmat, Apacked_krem, Bpacked_krem)
end
# Mrem
if Mrem > 0
Apacked_mrem_krem = pack_A_mrem_krem(Aptr, Val{mc}(), Ta, Mrem, Krem, Miter)
Cpmat_mrem = PtrMatrix{-1,nc}(gesp(Cptr, (Miter*mc, no*nc)), Mrem)
loopmul!(Cpmat_mrem, Apacked_mrem_krem, Bpacked_krem)
end
k = Krem
for ko in 1:Kiter
# pack kc x nc block of B
Bpacked = pack_B(Bptr, Val{kc}(), Val{nc}(), Tb, k, no)
for mo in 0:Miter-1
# pack mc x kc block of A
Apacked = pack_A(Aptr, Val{mc}(), Val{kc}(), Ta, mo, k)
Cpmat = PtrMatrix{mc,nc}(gesp(Cptr, (mo*mc, no*nc)))
loopmuladd!(Cpmat, Apacked, Bpacked)
end
# Mrem
if Mrem > 0
Apacked_mrem = pack_A_mrem(Aptr, Val{mc}(), Val{kc}(), Ta, Mrem, k, Miter)
Cpmat_mrem = PtrMatrix{-1,nc}(gesp(Cptr, (Miter*mc, no*nc)), Mrem)
loopmuladd!(Cpmat_mrem, Apacked_mrem, Bpacked)
end
k += kc
end
end
# Nrem
if Nrem > 0
# Krem
# pack kc x nc block of B
Bpacked_krem_nrem = pack_B_krem_nrem(Bptr, Val{kc}(), Val{nc}(), Tb, Krem, Nrem, Niter)
for mo in 0:Miter-1
# pack mc x kc block of A
Apacked_krem = pack_A_krem(Aptr, Val{mc}(), Ta, mo, Krem)
Cpmat_nrem = PtrMatrix{mc,-1}(gesp(Cptr, (mo*mc, Niter*nc)), Nrem)
loopmul!(Cpmat_nrem, Apacked_krem, Bpacked_krem_nrem)
end
# Mrem
if Mrem > 0
Apacked_mrem_krem = pack_A_mrem_krem(Aptr, Val{mc}(), Ta, Mrem, Krem, Miter)
Cpmat_mrem_nrem = PtrMatrix{-1,-1}(gesp(Cptr, (Miter*mc, Niter*nc)), Mrem, Nrem)
loopmul!(Cpmat_mrem_nrem, Apacked_mrem_krem, Bpacked_krem_nrem)
end
k = Krem
for ko in 1:Kiter
# pack kc x nc block of B
Bpacked_nrem = pack_B_nrem(Bptr, Val{kc}(), Val{nc}(), Tb, k, Nrem, Niter)
for mo in 0:Miter-1
# pack mc x kc block of A
Apacked = pack_A(Aptr, Val{mc}(), Val{kc}(), Ta, mo, k)
Cpmat_nrem = PtrMatrix{mc,-1}(gesp(Cptr, (mo*mc, Niter*nc)), Nrem)
loopmuladd!(Cpmat_nrem, Apacked, Bpacked_nrem)
end
# Mrem
if Mrem > 0
Apacked_mrem = pack_A_mrem(Aptr, Val{mc}(), Val{kc}(), Ta, Mrem, k, Miter)
Cpmat_mrem_nrem = PtrMatrix{-1,-1}(gesp(Cptr, (Miter*mc, Niter*nc)), Mrem, Nrem)
loopmuladd!(Cpmat_mrem_nrem, Apacked_mrem, Bpacked_nrem)
end
k += kc
end
end
end # GC.@preserve
C
end # functionIt's easier to follow if we assume all the GC.@preserve C A B LCACHE begin
for no in 0:Niter-1
k = Krem # pretending all the rems are 0
for ko in 1:Kiter
# pack kc x nc block of B
Bpacked = pack_B(Bptr, Val{kc}(), Val{nc}(), Tb, k, no)
for mo in 0:Miter-1
# pack mc x kc block of A
Apacked = pack_A(Aptr, Val{mc}(), Val{kc}(), Ta, mo, k)
Cpmat = PtrMatrix{mc,nc}(gesp(Cptr, (mo*mc, no*nc)))
loopmuladd!(Cpmat, Apacked, Bpacked)
end
k += kc
end
end
end # GC.@preserveThe three loops take steps of sizes LoopVectorization then takes care of the inner two most loops and microkernel: function loopmuladd!(
C::AbstractMatrix, A::AbstractMatrix, B::AbstractMatrix
)
M, K, N = matmul_sizes(C, A, B)
@avx for n ∈ 1:N, m ∈ 1:M
Cₘₙ = zero(eltype(C))
for k ∈ 1:K
Cₘₙ += A[m,k] * B[k,n]
dummy1 = prefetch0(A, m, k + 3)
end
C[m,n] += Cₘₙ
end
nothing
endto update a block of I still need to learn more about how TLBs work, but the basic idea behind packing is that it caches mappings of virtual memory addresses to physical memory addresses. But the TLB has a limited numbers of entries. If you access a lot of memory that is far apart, e.g. one column after another in arrays with large numbers of rows, the TLB cache won't be able to hold them all, and it will have to start calculating the mappings, stalling computation while the CPU waits for memory. Packing largely solves this by moving the memory close together. The TLB can store all the mappings of the packed submatrices, and then you reuse them many times. Packing also lets you do things like align the columns of Packing would also be when you switch to a struct of arrays representation (assuming the input isn't already a struct of arrays). The next major point is choosing julia> using PaddedMatrices: matmul_params
julia> matmul_params(Float64, Float64, Float64)
(200, 300, 600, 8)These aren't necessarilly optimal. You may need to experiment with them on your own computer. You can try different values with: @time jmul!(C1, A, B, Val(200), Val(300), Val(600), Val(0));Finally, the last consideration is prefetching memory. There is also a hardware prefetcher that triggers automatically. julia> M = round(Int, 65^2.2)
9737
julia> A = rand(M,M); B = rand(M,M); C1 = Matrix{Float64}(undef,M,M); C2 = similar(C1); C3 = similar(C1);
julia> @time jmul!(C1, A, B);
19.174104 seconds
julia> @time jmulh!(C2, A, B);
20.312452 seconds
julia> @time mul!(C3, A, B);
15.483092 seconds
julia> 2e-9 * M^3 / 19.174104 # jmul! single core GFLOPS
96.29204875002243
julia> 2e-9 * M^3 / 20.312452 # jmulh! single core GFLOPS
90.89566129711963
julia> 2e-9 * M^3 / 15.483092 # OpenBLAS single core GFLOPS
119.24709593574721Odds are LoopVectorization will need some modifications to do much better here. P.S. If you're on linux, you may want to make sure the OS is using transparent huge pages (so that one TLB entry maps to more addresses): julia> run(`cat /sys/kernel/mm/transparent_hugepage/enabled`); # path may be different based on distro
[always] madvise neverAlways is selected on my computer, but that may not be the default for every distribution. I think the default size for huge pages is 2MB (i.e., the size of a 512 x 512 matrix of |
I've been thinking a bit about which package we should put this nested loop-based implementation in. One option is to replace the divide-and-conquer implementation in Gaius.jl with the new implementation. I would prefer not to do this - I think it would be nice to keep the current implementation in Gaius for learning purposes, since it is a relatively straight-forward implementation. A second option is to keep the divide-and-conquer algorithm in Gaius.jl, and also add the nested loop algorithm to Gaius. Unfortunately, this will (1) complicated the Gaius codebase, and (2) will result in an even longer Gaius test-suite. I think, from a learning point of view, it makes more sense to keep the Gaius codebase simple. A third option is to put this algorithm into PaddedMatrices.jl. But, as Chris points out above, this code isn't specific to PaddedMatrices.jl, so it doesn't necessarily make sense for it to live there. The fourth option is to put the nested loop algorithm into its own package. (We can certainly borrow code from Gaius.jl, PaddedMatrices.jl, etc.) I've started work on option 4. I've created a package here: https://github.com/DilumAluthge/Augustus.jl The name is just a placeholder, and we can change it at any time. Any suggestions for the name? Now we just need to decide where this package lives. Options include:
What do y'all think? |
|
I don't particularly care where it lives. Another nice name, more in the vein of Gaius would be Octavian, but I don't have strong preferences. If you're going to write the package, I don't see why it shouldn't be owned by you. If it becomes useful, it may be a good idea to transfer it to JuliaLinearAlgebra |
|
What're the goals? The block sizes from this comment aren't that good, but it's an example implementation of the loop algorithm that doesn't take too many lines of code: Another library that may be worth looking at, and that doesn't use LoopVectorization for its primary kernels, is:
PaddedMatrices already has a fairly simple single threaded implementation, and I'm working on a multi-threaded implementation at the moment. |
I would say that for Octavian, it would be nice for the primary goal to be maximal performance. |
|
Moving to JuliaLinearAlgebra/Octavian.jl#19 |
That's what I like to hear! |
Here I wanted to talk about my experiments in PaddedMatrices.
I'd also suggest that if Gaius's performance were at least as good, I could use it and have PaddedMatrices mostly just define array types. My discussion of matmul here however will focus on Julia's base array type, rather than anything defined in PaddedMatrices -- which is why it'd make just as much sense for that code to live in a separate repo.
Although the implementation does currently make use of the
PtrArraytype defined inPaddedMatrices.Additionally, OpenBLAS's release notes suggested AVX512 and AVX2 should both be seeing much better performance with release 0.3.9 than 0.3.7 (which Julia is currently on), so I checkout this PR which upgrades Julia's OpenBLAS to 0.3.9:
JuliaLang/julia#35113
Hopefully it'll get merged to master soon (looks like AArch64 is having problems).
I'm seeing a phenomenal performance improvement by OpenBLAS on that release.
PaddedMatrices currently provides two different implementation approaches: jmul! and jmulh!. It also offers jmult!, which is a threaded version of
jmul!.The function's aren't too complicated. Should be straightforward to copy them here, if you'd like to change approaches.
Here is a plot of percent theoretical performance vs size:
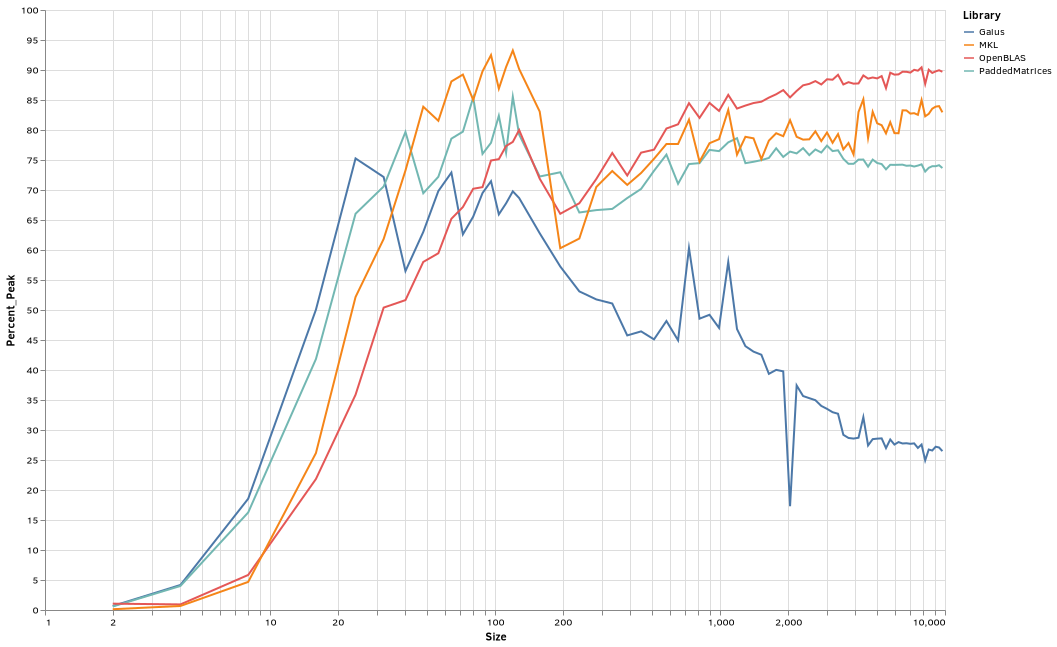
Interestingly, beyond around 200x200, OpenBLAS was now the fastest by a fairly comfortable margin.
It also looks like my implementation needs work. Aside from being slower than more OpenBLAS and MKL, it seems to slowly decline as size increases beyond 1000x1000, while OpenBLAS improves steadily and MKL sporadically.
But it's a marked improvement over Gaius on my computer -- hovering around 75% of peak CPU, while Gaius declined to barely more than a third of that by the largest tested sizes.
Script to generate the plot:
It could use some work on threading. It eventually hung -> crashed on interrupt, which is a known issue with multi threading on Julia master.
Results for the largest size:
Associated GFLOPS (peak is
min(num_cores, Threads.nthreads())times the single threaded peak; that was 18x in this case):So OpenBLAS and MKL were both close 88% at this point.
PaddedMatrices was at just under half the theoretical peak, and Gaius was at about 14%.
A lot of room for improvement in both cases.
PaddedMatrices is very slow to start using threads. In the copy and paste from when the benchmarks were running, Gaius was faster until 2191 x 2191 matrices, where they were equally fast, but by 4997 x 4997, PaddedMatrices was approaching twice as fast, and at 9737 it was three times faster -- but still far behind OpenBLAS and MKL.
MKL did very well with multi-threading, even at relatively small sizes.
jmult!could be modified to ramp up thread use more intelligently.The approach is summarized by this graphic:
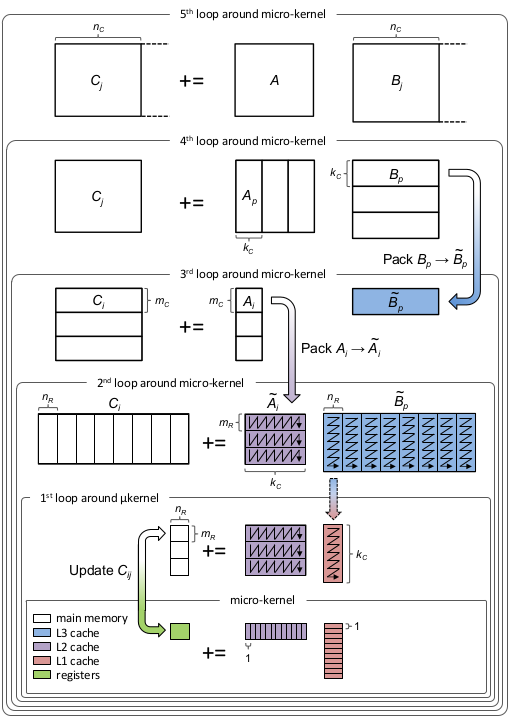
For which you can thank the BLIS team.
LoopVectorization takes care of the microkernel, and 2 loops around it.
So the
jmul!andjmult!functions add the other 3 loops (and also handle the remainders).The function
PaddedMatrices.matmul_paramsreturns themc,kc, andnc.I've also compiled BLIS, so I'll add it to future benchmarks as well.
The above BLIS loop link also talks about threading. BLIS threads any of the loops aside from the
kloop (I don't think you can multi-thread that one). 'PaddedMatrices.jmult!' threads both the 3rd and 5th. However, rather than threading in a smart way (i.e., in a manner reflecting the total number of threads), it spawns a new task for per iteration. When there are a lot of iterations, that's an excessive number of high-overhead tasks.On the otherhand, the outer most loop takes steps of size 600 on my computer -- which also means it takes a long time before it uses many threads at all.
Would you be in favor of replacing the name-sake recursive implementation with this nested loop-based GEMM implementation?
The text was updated successfully, but these errors were encountered: