|
1 | 1 | --- |
2 | | -Title: 'Binary Search Algorithm' |
3 | | -Description: 'An efficient searching algorithm' |
| 2 | +Title: 'Binary Search' |
| 3 | +Description: 'Binary search is an effective searching algorithm for finding an element within a sorted collection of items.' |
4 | 4 | Subjects: |
5 | | - - 'Computer Science' |
6 | 5 | - 'Code Foundations' |
| 6 | + - 'Computer Science' |
7 | 7 | Tags: |
8 | 8 | - 'Algorithms' |
| 9 | + - 'Arrays' |
9 | 10 | - 'Data Structures' |
10 | 11 | - 'Search Algorithms' |
11 | 12 | CatalogContent: |
12 | 13 | - 'learn-python-3' |
13 | 14 | - 'paths/computer-science' |
14 | 15 | --- |
15 | 16 |
|
16 | | -**Binary Search** is an algorithm for searching an element within a sorted collection of items, primarily implemented with [arrays](https://www.codecademy.com/resources/docs/general/data-structures/array) or lists. The binary search algorithm follows a divide-and-conquer approach by repeatedly dividing the collection into two halves and comparing the target value with the middle element of the current search space. If there is a match, it provides the index of the middle element; otherwise, it proceeds to either side of the array, depending on the current comparison result. |
| 17 | +**Binary search** is an effective searching algorithm for finding an element within a sorted collection of items, primarily implemented with [arrays](https://www.codecademy.com/resources/docs/general/data-structures/array) or lists. The binary search algorithm follows a divide-and-conquer approach by repeatedly dividing the collection into two halves and comparing the target value with the middle element of the current search space. If there is a match, it provides the index of the middle element; otherwise, it proceeds to either side of the array, depending on the current comparison result. |
17 | 18 |
|
18 | | -> **Note**: The collection must be sorted and have constant time indexing such as arrays to implement the binary search algorithm. Binary search is incompatible with data structures that do not support constant-time indexing. |
| 19 | +> **Note:** To implement the binary search algorithm, the collection must be sorted and have constant-time indexing, such as arrays. Binary search is incompatible with [data structures](https://www.codecademy.com/resources/docs/general/data-structures) that do not support constant-time indexing. |
19 | 20 |
|
20 | | -## The Algorithm |
| 21 | +## How Binary Search Works |
21 | 22 |
|
22 | | -The steps for the binary search algorithm are as follows: |
| 23 | +Here are the steps for the binary search algorithm: |
23 | 24 |
|
24 | | -1. Set the `start` pointer to the beginning of the collection (index 0). |
25 | | -2. Set the `end` pointer to the end of the collection (length(collection) - 1). |
| 25 | +1. Set the `start` pointer to the beginning of the collection (index `0`). |
| 26 | +2. Set the `end` pointer to the end of the collection (`length(collection) - 1`). |
26 | 27 | 3. While the `start` is less than or equal to the `end` pointer, repeat these steps: |
27 | 28 | 1. Calculate the middle element index: `mid = start + (end - start) / 2`. |
28 | | - 2. Compare the value at middle index (`mid`) with the target value. |
29 | | - 1. If `arr[mid]` is equal to the target value, return `mid` (search successful). |
| 29 | + 2. Compare the value at the middle index (`mid`) with the target value. |
| 30 | + 1. If `arr[mid]` equals the target value, return `mid` (search successful). |
30 | 31 | 2. If `arr[mid]` is less than the target value, set the `start` to `mid + 1`. |
31 | | - 3. If `arr[mid]` is greater than the target value, set the `end` to `mid - 1`. |
32 | | -4. If the `start` pointer becomes greater than the `end` pointer, the target value is not in the collection. Return `-1` to indicate that the target is not present. |
| 32 | + 3. If `arr[mid]` exceeds the target value, set the `end` to `mid - 1`. |
| 33 | +4. The target value is not in the collection if the `start` pointer becomes greater than the `end` pointer. Return `-1` to indicate that the target is not present. |
33 | 34 |
|
34 | | -## Complexities for Binary Search Algorithm |
| 35 | +## Example of Binary Search |
35 | 36 |
|
36 | | -### Time Complexity |
| 37 | +This example implements the binary search algorithm for searching the number `9` in the sorted array `[1, 3, 4, 6, 8, 9, 11]`. |
37 | 38 |
|
38 | | -- Average Case: `O(log n)` |
39 | | -- Worst Case: `O(log n)` |
40 | | -- Best Case: `O(1)` |
| 39 | +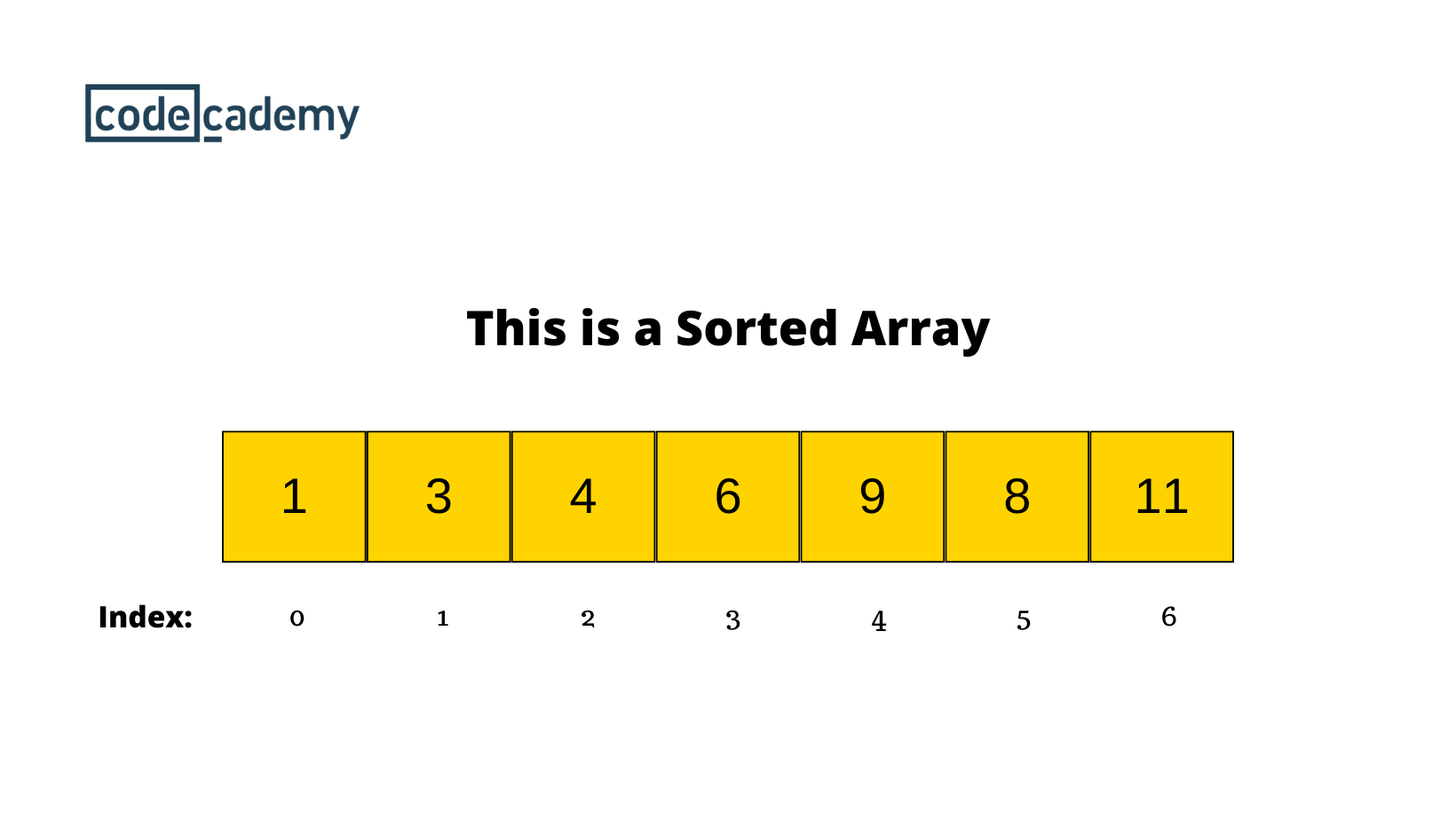 |
41 | 40 |
|
42 | | -The binary search algorithm has logarithmic time complexity because it divides the array repeatedly until the target element is discovered or the search space is empty. |
| 41 | +In the first iteration, `start` is at `0`, `end` is at `6`, and `mid` becomes `3` after calculating. The algorithm compares `mid` to the target value. Since the target value (`9`) is greater than the middle element (`6`), the algorithm proceeds with the search to the right half by updating the `start` index to `mid + 1`, which is `4`. Now, the algorithm will focus on finding the target value in the array's right portion (index `4` to `6`). |
43 | 42 |
|
44 | | -In the worst-case scenario, the target element does not exist in the collection. In such cases, the algorithm keeps dividing the collection until it has exhausted the search space. |
| 43 | +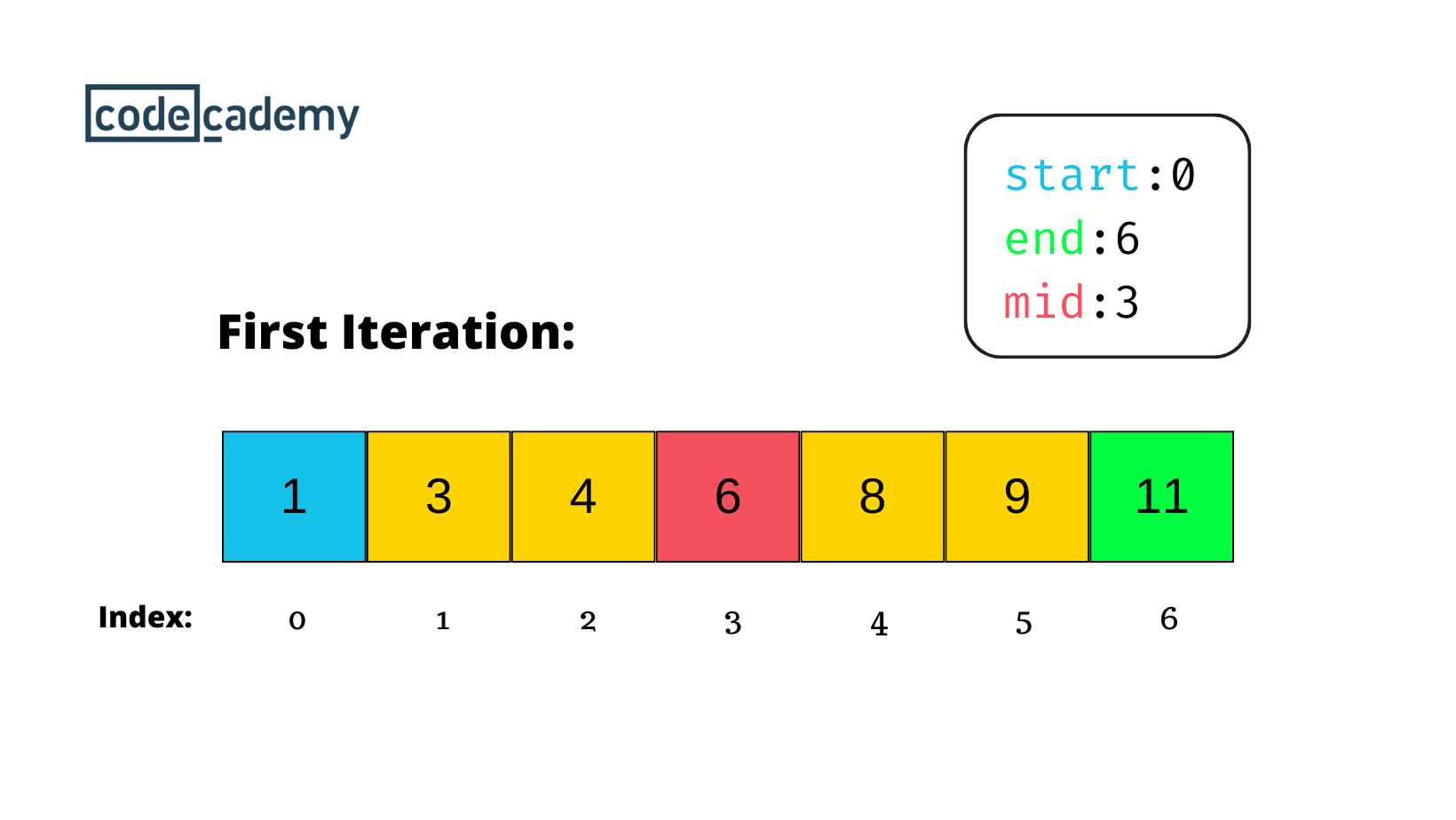 |
45 | 44 |
|
46 | | -### Space Complexity |
| 45 | +In the second iteration, `mid` becomes `5`, the index of the target value (`9`). Since the target value is equal to the `mid`, the algorithm identifies the element's position. |
47 | 46 |
|
48 | | -Binary search has a space complexity of `O(1)` as it is a space-efficient algorithm. |
| 47 | +However, the search is not instantly completed; the algorithm changes the search range. In this case, the `start` index is set to `mid + 1`, which starts a narrowed search on the right part of the array. |
49 | 48 |
|
50 | | -## Example |
| 49 | +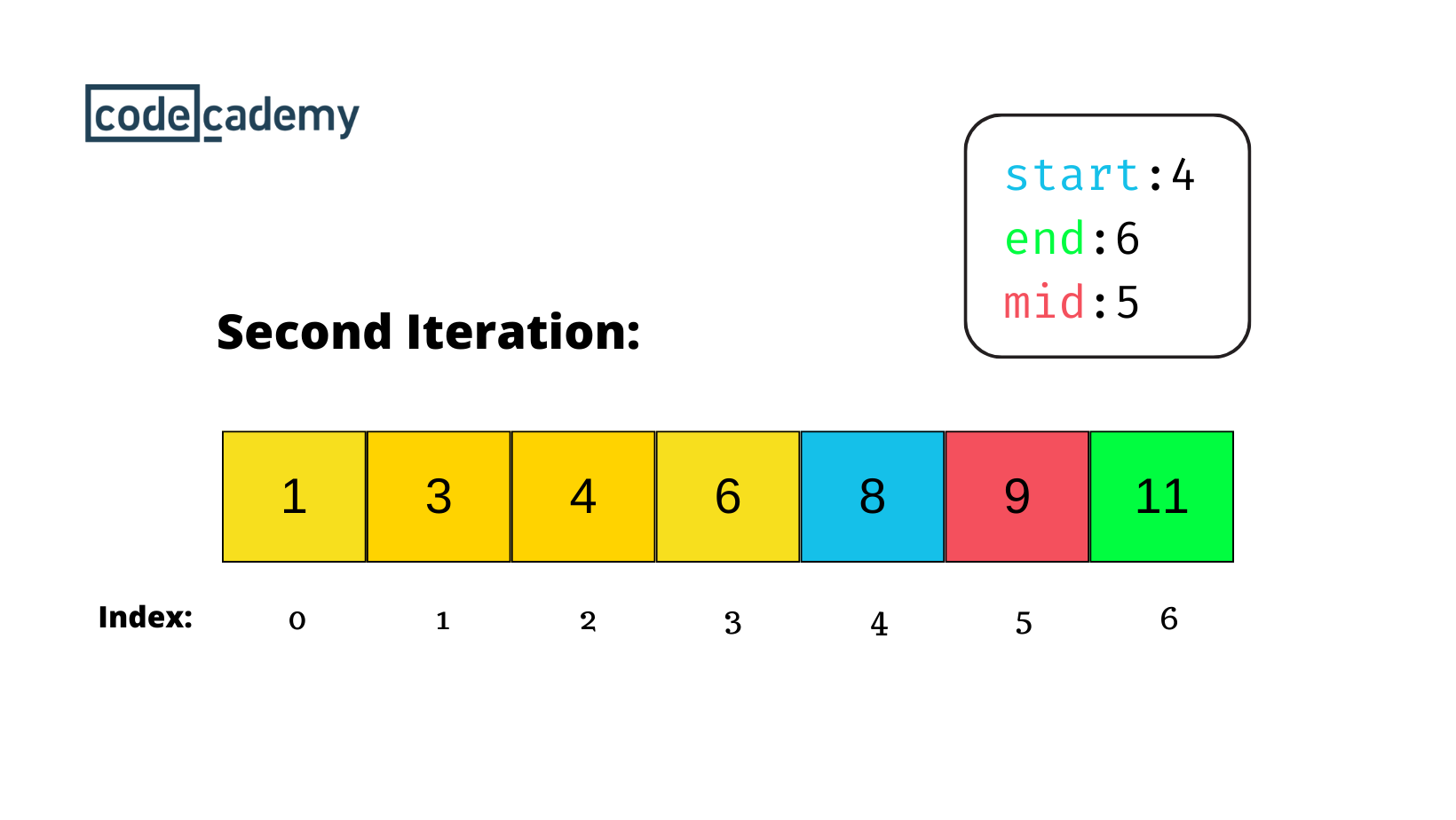 |
51 | 50 |
|
52 | | -In the example below, a sorted array has elements such as `[1, 3, 4, 6, 8, 9, 11]`. The aim is to implement the binary search algorithm for searching the number `9`. |
| 51 | +In the last iteration, the binary search algorithm narrowed the search to a single element. The middle indexes `mid`, `start`, and `end` now point directly to the target value (`9`). |
53 | 52 |
|
54 | | - |
| 53 | +The algorithm recognizes the match, and the search concludes that the target value is found at index `5` and the binary search is successful. |
55 | 54 |
|
56 | | -In the first iteration, `start` is at 0, `end` is at 6, and `mid` becomes 3 after calculating. The algorithm compares `mid` to the target value. Since the target value (9) is greater than the middle element (6), the algorithm proceeds the search to the right half by updating the `start` index to `mid + 1`, which is 4. Now, the algorithm will focus on finding the target value in the array's right portion(index 4 to 6). |
| 55 | +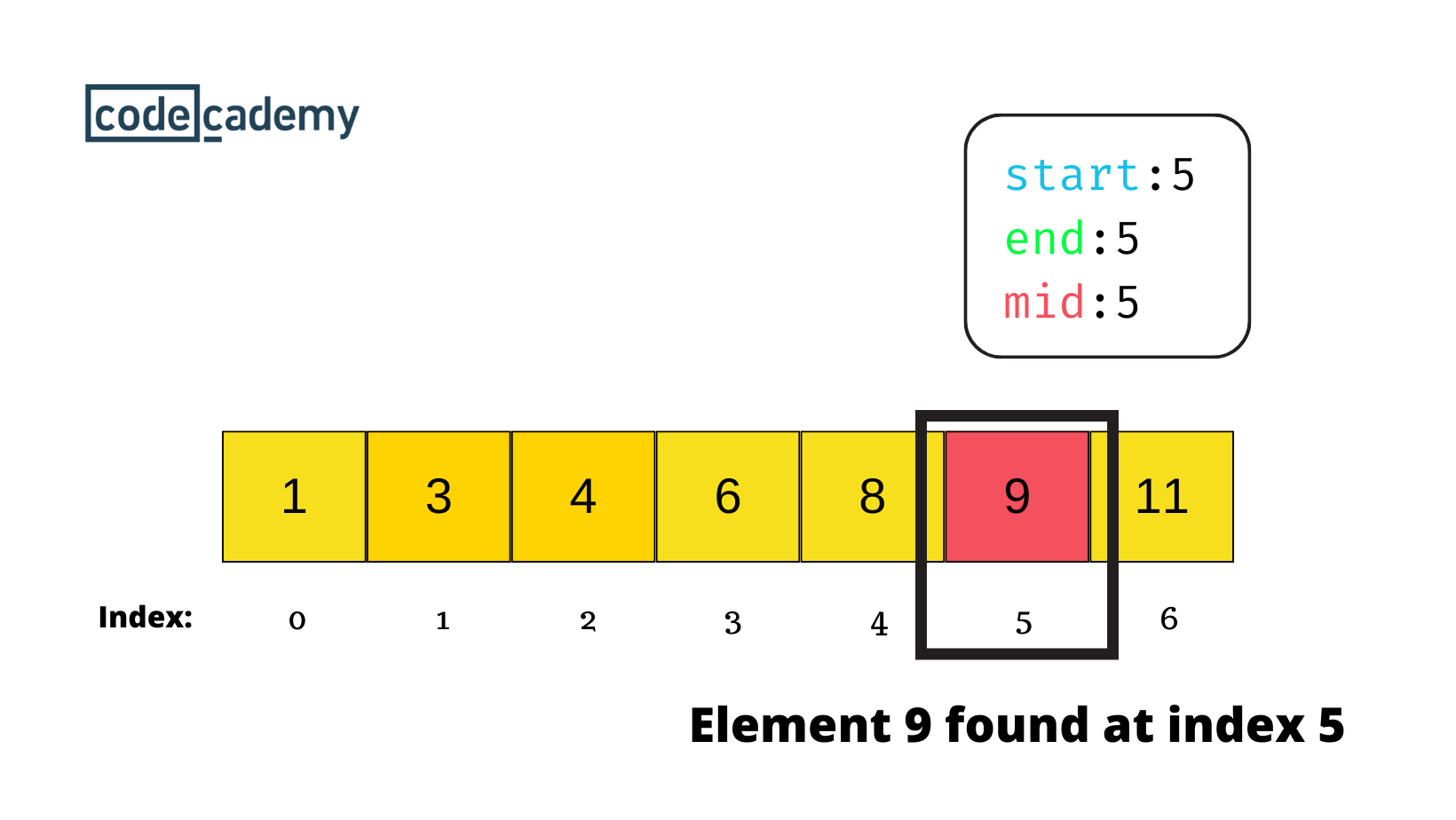 |
57 | 56 |
|
58 | | - |
| 57 | +## Implementation of Binary Search |
59 | 58 |
|
60 | | -In the second iteration, `mid` becomes 5, which is the index of the target value (9). Since the target value is equal to the `mid`, the algorithm identifies the element's position. |
| 59 | +This example shows the implementation of binary search in [Python](https://www.codecademy.com/resources/docs/python): |
61 | 60 |
|
62 | | -However, the search is not instantly completed; instead, the algorithm changes the search range. In this case, the `start` index is set to `mid + 1` which starts a narrowed search on the right part of the array. |
| 61 | +```py |
| 62 | +def binary_search(arr, target): |
| 63 | + left, right = 0, len(arr) - 1 |
63 | 64 |
|
64 | | - |
| 65 | + while left <= right: |
| 66 | + mid = (left + right) // 2 |
65 | 67 |
|
66 | | -In the last iteration, the binary search algorithm has narrowed down the search to a single element. The middle index `mid`, `start`, and `end`, are now pointing directly to the target value (9). |
| 68 | + if arr[mid] == target: |
| 69 | + return mid # Target found |
| 70 | + elif arr[mid] < target: |
| 71 | + left = mid + 1 |
| 72 | + else: |
| 73 | + right = mid - 1 |
67 | 74 |
|
68 | | -The algorithm recognizes the match, and the search concludes that the target value is found at index 5 and the binary search is successful. |
| 75 | + return -1 # Target not found |
69 | 76 |
|
70 | | - |
| 77 | +# Example usage |
| 78 | +numbers = [1, 4, 6, 7, 9, 11, 13, 15] |
| 79 | +target_value = 7 |
| 80 | + |
| 81 | +result = binary_search(numbers, target_value) |
| 82 | + |
| 83 | +if result != -1: |
| 84 | + print(f"Element {target_value} found at index {result}.") |
| 85 | +else: |
| 86 | + print(f"Element {target_value} not found in the array.") |
| 87 | +``` |
| 88 | + |
| 89 | +This example searches for the number `7` in the array `numbers`. Since `7` exists in the array, the output for the example will be: |
| 90 | + |
| 91 | +```shell |
| 92 | +Element 7 found at index 3. |
| 93 | +``` |
| 94 | + |
| 95 | +## Time Complexity of Binary Search |
| 96 | + |
| 97 | +Here's a detailed look at the time complexity of binary search across different scenarios: |
| 98 | + |
| 99 | +**Best-Case Time Complexity:** |
| 100 | + |
| 101 | +The best case occurs when the target element is at the middle of the array during the first comparison. In this case, the algorithm finds the target immediately, completing the search in just one step. This results in a time complexity of _O(1)_, or constant time. |
| 102 | + |
| 103 | +**Average-Case Time Complexity:** |
| 104 | + |
| 105 | +On average, binary search reduces the search space by half with each iteration. After each comparison, it discards one half of the array and continues searching the remaining half. As a result, the number of steps required grows logarithmically with the number of elements, giving it an average time complexity of _O(log n)_. |
| 106 | + |
| 107 | +**Worst-Case Time Complexity:** |
| 108 | + |
| 109 | +The worst-case scenario occurs when the algorithm must continue halving the array until only one element is left to check—this occurs when the target is either not present in the array or is located at the end of the search process. Even in this scenario, the time complexity remains \_O(log n)\_since each iteration still halves the search interval. |
| 110 | + |
| 111 | +## Space Complexity of Binary Search |
| 112 | + |
| 113 | +The space complexity of binary search depends on whether it is implemented iteratively or recursively, but in both cases, it is highly efficient, making it ideal for memory-constrained applications. |
| 114 | + |
| 115 | +**Iterative Implementation:** |
| 116 | + |
| 117 | +When implemented using a loop, binary search requires only a constant amount of extra space. It uses a few variables - typically for the low, high, and mid indices - to keep track of the current portion of the array being searched. No additional memory is needed proportional to the size of the input. This results in a space complexity of _O(1)_. |
| 118 | + |
| 119 | +**Recursive Implementation:** |
| 120 | + |
| 121 | +Each function call adds a new frame to the call stack in a recursive implementation. Because the array is divided in half at each step, the maximum depth of recursion is _log n_, where `n` refers to the length of the array. Thus, the space complexity becomes _O(log n)_ due to the stack frames created by recursion. |
| 122 | + |
| 123 | +## Binary Search vs. Other Searching Algorithms |
| 124 | + |
| 125 | +This table compares the time and space complexity of binary search with other searching algorithms: |
| 126 | + |
| 127 | +| **Algorithm** | **Best-Case Time Complexity** | **Average-Case Time Complexity** | **Worst-Case Time Complexity** | **Space Complexity** | |
| 128 | +| ---------------------- | ----------------------------- | -------------------------------- | ------------------------------ | -------------------- | |
| 129 | +| **Binary Search** | O(1) | O(log n) | O(log n) | O(1) / O(log n) | |
| 130 | +| **Linear Search** | O(1) | O(n) | O(n) | O(1) | |
| 131 | +| **Jump Search** | O(1) | O(√n) | O(√n) | O(1) | |
| 132 | +| **Exponential Search** | O(1) | O(log n) | O(log n) | O(1) | |
| 133 | + |
| 134 | +## Frequently Asked Questions |
| 135 | + |
| 136 | +### 1. Can binary search be used on unsorted arrays? |
| 137 | + |
| 138 | +No, binary search only works on sorted arrays. If the array is not sorted, the algorithm cannot reliably determine which half of the array to search next, making the process ineffective. |
| 139 | + |
| 140 | +### 2. What is the difference between binary search and linear search? |
| 141 | + |
| 142 | +The main difference lies in efficiency: |
| 143 | + |
| 144 | +- Binary search divides the search range in half each time and has a time complexity of _O(log n)_, helping it operate much faster for large, sorted lists. |
| 145 | +- Linear search verifies each element individually and has a time complexity of _O(n)_. |
| 146 | + |
| 147 | +### 3. Is binary search suitable for linked lists? |
| 148 | + |
| 149 | +Not typically. Although you can perform binary search on a linked list, it is inefficient because linked lists do not support constant-time indexing. Accessing the middle element takes linear time, defeating the algorithm’s efficiency purpose. |
0 commit comments