|
1 | 1 | --- |
2 | 2 | Title: 'Postorder Traversal' |
3 | | -Description: 'First traverses the left subtree, then the right subtree, and then the root.' |
| 3 | +Description: 'Performs a tree traversal that visits the left subtree, right subtree, and then the root node.' |
4 | 4 | Subjects: |
5 | 5 | - 'Computer Science' |
6 | 6 | - 'Code Foundations' |
7 | 7 | Tags: |
8 | 8 | - 'Algorithms' |
9 | | - - 'Conceptual' |
10 | 9 | - 'Binary Tree' |
| 10 | + - 'Conceptual' |
11 | 11 | - 'Data Structures' |
12 | 12 | - 'Search' |
13 | 13 | - 'Trees' |
14 | 14 | CatalogContent: |
15 | | - - 'complex-data-structures' |
| 15 | + - 'learn-python-3' |
16 | 16 | - 'paths/computer-science' |
17 | 17 | --- |
18 | 18 |
|
19 | | -**Postorder traversal** is a depth-first search [algorithm](https://www.codecademy.com/resources/docs/general/algorithm) for a binary search tree that first traverses the left subtree, then the right subtree, and then the root. Its primary use is deleting the tree. |
| 19 | +**Postorder traversal** is a depth-first tree traversal [algorithm](https://www.codecademy.com/resources/docs/general/algorithm) where each node is visited in a specific sequence: left subtree, right subtree, and finally the root node. This traversal technique recursively processes all children of a node before processing the node itself, making it especially useful for operations that require bottom-up processing. |
| 20 | + |
| 21 | +Postorder traversal has several important applications in computer science and data processing. It's commonly used for deleting trees (since children must be deleted before their parent nodes), evaluating postfix expressions, and calculating directory sizes in file systems. When applied to expression trees, postorder traversal naturally produces postfix notation, which is valuable in compiler design and expression evaluation. |
20 | 22 |
|
21 | 23 | ## Algorithm |
22 | 24 |
|
23 | | -The postorder algorithm can be described as follows: |
| 25 | +To perform a postorder traversal of a binary tree: |
24 | 26 |
|
25 | | -```pseudo |
26 | | -Function Postorder(tree) |
27 | | - return Postorder(left-subtree) + Postorder(right-subtree) + root |
28 | | -``` |
| 27 | +1. Recursively traverse the left subtree |
| 28 | +2. Recursively traverse the right subtree |
| 29 | +3. Visit the root node |
| 30 | + |
| 31 | +For a general tree (where nodes can have more than two children): |
29 | 32 |
|
30 | | -## Example |
| 33 | +1. Recursively traverse all children from left to right |
| 34 | +2. Visit the root node |
31 | 35 |
|
32 | | -For the following binary search tree: |
| 36 | +Post order traversal returns a sequence of node values that represents the order in which nodes were visited. For the following binary search tree: |
33 | 37 |
|
34 | 38 | 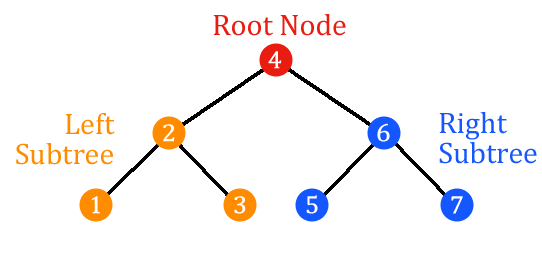 |
35 | 39 |
|
36 | 40 | Postorder traversal provides the nodes in the following order: `1`, `3`, `2`, `5`, `7`, `6`, `4`. |
| 41 | + |
| 42 | +## Example 1: Basic Post Order Traversal Using Python |
| 43 | + |
| 44 | +This example demonstrates how to implement a simple post order traversal of a binary tree using recursion in Python: |
| 45 | + |
| 46 | +```py |
| 47 | +class TreeNode: |
| 48 | + def __init__(self, value): |
| 49 | + self.value = value |
| 50 | + self.left = None |
| 51 | + self.right = None |
| 52 | + |
| 53 | +def post_order_traversal(root): |
| 54 | + """ |
| 55 | + Performs a post order traversal of a binary tree. |
| 56 | +
|
| 57 | + Args: |
| 58 | + root: The root node of the binary tree |
| 59 | +
|
| 60 | + Returns: |
| 61 | + A list containing node values in post order |
| 62 | + """ |
| 63 | + result = [] |
| 64 | + |
| 65 | + # Helper function for recursion |
| 66 | + def traverse(node): |
| 67 | + # Base case: if node is None, return |
| 68 | + if node is None: |
| 69 | + return |
| 70 | + |
| 71 | + # First, visit left subtree |
| 72 | + traverse(node.left) |
| 73 | + |
| 74 | + # Then, visit right subtree |
| 75 | + traverse(node.right) |
| 76 | + |
| 77 | + # Finally, visit the node itself (add to result) |
| 78 | + result.append(node.value) |
| 79 | + |
| 80 | + # Start traversal from root |
| 81 | + traverse(root) |
| 82 | + return result |
| 83 | + |
| 84 | +# Example usage |
| 85 | +if __name__ == "__main__": |
| 86 | + # Create a simple binary tree |
| 87 | + # 1 |
| 88 | + # / \ |
| 89 | + # 2 3 |
| 90 | + # / \ |
| 91 | + # 4 5 |
| 92 | + |
| 93 | + root = TreeNode(1) |
| 94 | + root.left = TreeNode(2) |
| 95 | + root.right = TreeNode(3) |
| 96 | + root.left.left = TreeNode(4) |
| 97 | + root.left.right = TreeNode(5) |
| 98 | + |
| 99 | + # Perform post order traversal |
| 100 | + result = post_order_traversal(root) |
| 101 | + print("Post order traversal:", result) |
| 102 | +``` |
| 103 | + |
| 104 | +Output generated by this code will be: |
| 105 | + |
| 106 | +```shell |
| 107 | +Post order traversal: [4, 5, 2, 3, 1] |
| 108 | +``` |
| 109 | + |
| 110 | +In this example, we traverse the tree in postorder: left subtree (4, 5, 2), then right subtree (3), and finally the root (1). The output demonstrates that postorder traversal visits children before their parent nodes. |
| 111 | + |
| 112 | +## Example 2: Iterative Post Order Traversal Using Python |
| 113 | + |
| 114 | +This example shows how to implement postorder traversal without recursion, using an iterative approach with two stacks in Python: |
| 115 | + |
| 116 | +```py |
| 117 | +class TreeNode: |
| 118 | + def __init__(self, value): |
| 119 | + self.value = value |
| 120 | + self.left = None |
| 121 | + self.right = None |
| 122 | + |
| 123 | +def iterative_post_order(root): |
| 124 | + """ |
| 125 | + Performs a post order traversal of a binary tree iteratively using two stacks. |
| 126 | +
|
| 127 | + Args: |
| 128 | + root: The root node of the binary tree |
| 129 | +
|
| 130 | + Returns: |
| 131 | + A list containing node values in post order |
| 132 | + """ |
| 133 | + if not root: |
| 134 | + return [] |
| 135 | + |
| 136 | + result = [] |
| 137 | + stack1 = [root] # First stack for traversal |
| 138 | + stack2 = [] # Second stack to store post order |
| 139 | + |
| 140 | + # Process all nodes |
| 141 | + while stack1: |
| 142 | + node = stack1.pop() |
| 143 | + stack2.append(node) |
| 144 | + |
| 145 | + if node.left: |
| 146 | + stack1.append(node.left) |
| 147 | + if node.right: |
| 148 | + stack1.append(node.right) |
| 149 | + |
| 150 | + while stack2: |
| 151 | + node = stack2.pop() |
| 152 | + result.append(node.value) |
| 153 | + |
| 154 | + return result |
| 155 | + |
| 156 | +# Example usage |
| 157 | +if __name__ == "__main__": |
| 158 | + # Create a binary tree |
| 159 | + # 1 |
| 160 | + # / \ |
| 161 | + # 2 3 |
| 162 | + # / \ \ |
| 163 | + # 4 5 6 |
| 164 | + |
| 165 | + root = TreeNode(1) |
| 166 | + root.left = TreeNode(2) |
| 167 | + root.right = TreeNode(3) |
| 168 | + root.left.left = TreeNode(4) |
| 169 | + root.left.right = TreeNode(5) |
| 170 | + root.right.right = TreeNode(6) |
| 171 | + |
| 172 | + result = iterative_post_order(root) |
| 173 | + print("Iterative post order traversal:", result) |
| 174 | +``` |
| 175 | + |
| 176 | +The output of this code will be: |
| 177 | + |
| 178 | +```shell |
| 179 | +Iterative post order traversal: [4, 5, 2, 6, 3, 1] |
| 180 | +``` |
| 181 | + |
| 182 | +This example demonstrates an alternative non-recursive approach to postorder traversal. The iterative solution is particularly useful when dealing with deep trees where recursive approaches might cause stack overflow issues. |
| 183 | + |
| 184 | +## Codebyte Example: Calculating Directory Size Using Python |
| 185 | + |
| 186 | +This example demonstrates a practical application of postorder traversal for calculating the total size of directories in a file system using Python: |
| 187 | + |
| 188 | +```py |
| 189 | +class FileNode: |
| 190 | + def __init__(self, name, is_directory=False, size=0): |
| 191 | + self.name = name |
| 192 | + self.is_directory = is_directory |
| 193 | + self.size = size # Size in bytes (only for files) |
| 194 | + self.children = [] # For directories, list of files/subdirectories |
| 195 | + |
| 196 | +def calculate_directory_sizes(root): |
| 197 | + """ |
| 198 | + Calculate sizes of all directories using post order traversal. |
| 199 | +
|
| 200 | + Args: |
| 201 | + root: Root directory node |
| 202 | +
|
| 203 | + Returns: |
| 204 | + Dictionary mapping directory names to their total sizes |
| 205 | + """ |
| 206 | + directory_sizes = {} |
| 207 | + |
| 208 | + def traverse(node): |
| 209 | + # Base case: if it's a file, return its size |
| 210 | + if not node.is_directory: |
| 211 | + return node.size |
| 212 | + |
| 213 | + # For directories, calculate total size from children |
| 214 | + total_size = 0 |
| 215 | + |
| 216 | + # Visit all children first (post order) |
| 217 | + for child in node.children: |
| 218 | + total_size += traverse(child) |
| 219 | + |
| 220 | + # Store the directory's total size |
| 221 | + directory_sizes[node.name] = total_size |
| 222 | + return total_size |
| 223 | + |
| 224 | + # Start traversal from root directory |
| 225 | + traverse(root) |
| 226 | + return directory_sizes |
| 227 | + |
| 228 | +# Example usage |
| 229 | +if __name__ == "__main__": |
| 230 | + # Create a sample file system structure |
| 231 | + # root (dir) |
| 232 | + # / \ |
| 233 | + # docs (dir) images (dir) |
| 234 | + # / \ / \ |
| 235 | + # f1.txt f2.txt img1.jpg img2.jpg |
| 236 | + |
| 237 | + root = FileNode("root", is_directory=True) |
| 238 | + |
| 239 | + docs = FileNode("docs", is_directory=True) |
| 240 | + f1 = FileNode("f1.txt", size=100) # 100 bytes |
| 241 | + f2 = FileNode("f2.txt", size=200) # 200 bytes |
| 242 | + docs.children = [f1, f2] |
| 243 | + |
| 244 | + images = FileNode("images", is_directory=True) |
| 245 | + img1 = FileNode("img1.jpg", size=500) # 500 bytes |
| 246 | + img2 = FileNode("img2.jpg", size=700) # 700 bytes |
| 247 | + images.children = [img1, img2] |
| 248 | + |
| 249 | + root.children = [docs, images] |
| 250 | + |
| 251 | + # Calculate directory sizes |
| 252 | + sizes = calculate_directory_sizes(root) |
| 253 | + |
| 254 | + # Display results |
| 255 | + for directory, size in sizes.items(): |
| 256 | + print(f"{directory}: {size} bytes") |
| 257 | +``` |
| 258 | + |
| 259 | +This example illustrates how postorder traversal naturally solves the problem of calculating directory sizes. Since knowledge of the sizes of all subdirectories is needed before calculating the size of a parent directory, postorder traversal ensures processing of children occurs before processing of parents. |
| 260 | + |
| 261 | +## Frequently Asked Questions |
| 262 | + |
| 263 | +### 1. What is the difference between preorder, in-order, and postorder traversal? |
| 264 | + |
| 265 | +- Preorder: Visit root, then left subtree, then right subtree (Root → Left → Right) |
| 266 | +- Inorder: Visit left subtree, then root, then right subtree (Left → Root → Right) |
| 267 | +- Postorder: Visit left subtree, then right subtree, then root (Left → Right → Root) |
| 268 | + |
| 269 | +### 2. What is the time complexity of postorder traversal? |
| 270 | + |
| 271 | +The time complexity is O(n), where n is the number of nodes in the tree, as each node is visited exactly once. |
| 272 | + |
| 273 | +### 3. What is the space complexity of postorder traversal? |
| 274 | + |
| 275 | +- For recursive implementation: O(h) where h is the height of the tree (due to the recursion stack) |
| 276 | +- For iterative implementation with stacks: O(n) in the worst case |
| 277 | + |
| 278 | +### 4. When should I use postorder traversal instead of other traversal methods? |
| 279 | + |
| 280 | +- Use postorder traversal when you need to process child nodes before their parent nodes |
| 281 | +- Common applications include tree deletion, evaluating postfix expressions, and bottom-up computations |
| 282 | + |
| 283 | +### 5. Can postorder traversal be used for non-binary trees? |
| 284 | + |
| 285 | +Yes, postorder traversal can be generalized to n-ary trees by visiting all children before the parent node |
0 commit comments