相同的数字按位或等于0,任何数字和0进行按位或操作都等于那个数字。
高位到低位:高位乘2加低位,在乘2加下一位。
使用一个队列来实现,先把根节点入队,在每次让父节点出队的同时,让子节点入队。
一次性遍历到二叉树的叶子结点,再往回访问。深度优先遍历又分为前序遍历,中序遍历和后序遍历。
二叉搜索树的中序遍历是一个从小到大递增的序列。
二叉搜索树的验证,在验证某个结点时,需要验证这个结点是否在某个范围内,而不仅仅是大于/小于父节点。一般与父节点的父节点有关
Arrays.fill(arr,XXX) 把数组里的元素全部赋值为某一个值。
可以先枚举区间长度
一般使用二维数组记录区间的起始和结束,有时候可能要用到三维以上
求链表倒数第k个:不需要计算长度,先让前指针走k,再让后指针跟着前指针一起走,前指针走到底的时候后指针的值就是倒数第k个了。
寻找链表是否为环形链表,或者寻找链表的中点,都可以使用快慢指针。一个指针每次走一格,另一个快指针每次走两格,快指针走到终点的时候,慢指针刚好走到中间部分。
逆序处理(链表数相加)的时候可以用。
适用于找重复元素,或是环形表的环节店。如果add失败说明哈希表中含有该元素。
一种双端队列,可以从栈底出栈。
Deque deque= new LinkedList<>();
使用队列来实现该方法,当窗口满足要求时(比如窗口内的元素不重复等),添加元素,不满足要求时就需要适当的==移除一部分元素==。最后求得某个状态下窗口的某个最好的属性(长度等)。
适用题目:3.无重复字符的最长字串https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
寻找两个数组合并后第k小的数,可以先比较两个数组中的==k/2的位置==的元素大小。对于较小的那个数组,前面k/2个元素==一定不包含==需要找的第k小的数,因此把前面的数全部删掉,同时k应该要发生相应的改变(减去那些数的个数)。以此类推,k/2是我们每次要删除的元素的个数,最后k/2=0时得到第k小的数。此时这个数是剩下的数中最小的。
方便合并链表或是其他对链表的操作,使用一个前置的哨兵节点指向操作后链表的第一个节点,这样就可以省去首个节点的判断步骤,节省代码。
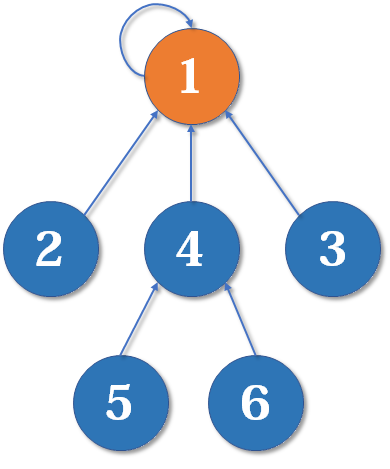
采取(先序)遍历的方式,对每个结点用HashMap<Integer,TreeNode>保存(每个结点的值唯一),键对应的是结点的值,TreeNode对应的就是他的父亲结点。通过对map不断get可以最终找到root。
前缀和的相反形式,差分数组的第i个数即为原数组的第i-1个元素和第i个元素的差值,也就是说我们对差分数组求前缀和即可得到原数组。
需要对某个区间做增量时,对于差分数组,让区间最左加上增量,最右+1的位置减去一个增量,最后求前缀和就能得到答案。
主要用于解决一些元素分组问题。管理一系列不相交的集合。支持集合的合并与查询。
并查集是一个树状结构,一个树状结构就是一个集合,每一个树状结构的root根就是这个并查集的代表,他的子节点最终都指向它。要寻找集合代表的元素,只需要对子节点一层一层往上访问父节点。根节点的父节点是他自己。
存储:可以用数组的形式来保存一个并查集。每一个元素的值是它父节点的索引(index)。
按秩(rank)合并:把简单的树放复杂的树上合并(这样合并后到根节点距离边长的结点个数比较少)。用一个数组记录每个根节点对应的树的深度。在合并时,把rank较小的往rank较大的结点上合并。
//初始化
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
{
fa[i] = i;
rank[i] = 1;
}
}
//合并
inline void merge(int i, int j)
{
int x = find(i), y = find(j); //先找到两个根节点
if (rank[x] <= rank[y])
fa[x] = y;
else
fa[y] = x;
if (rank[x] == rank[y] && x != y)
rank[y]++; //如果深度相同且根节点不同,则新的根节点的深度+1
}能够满足任意两点之间有且仅有一条简单路径只有树,且这棵树包含n个节点。我们称这棵树为给定的图的生成树,其中总权值最小的生成树,我们称其为最小生成树。
Kruskal 算法是一种常见并且好写的最小生成树算法,由 \text{Kruskal}Kruskal 发明。该算法的基本思想是从小到大加入边,是一个贪心算法。
其算法流程为:
-
将图 G={V,E}G={V,E} 中的所有边按照长度由小到大进行排序,等长的边可以按任意顺序。
-
初始化图 G'G为{V,∅},从前向后扫描排序后的边,如果扫描到的边e在 G'G 中连接了两个相异的连通块,则将它插入G'G中。
-
最后得到的图 G'G 就是图 GG 的最小生成树。
在实际代码中,我们首先将这张完全图中的边全部提取到边集数组中,然后对所有边进行排序,从小到大进行枚举,每次贪心选边加入答案。使用并查集维护连通性,若当前边两端不连通即可选择这条边。
把众数记为+1,其它数记为-1。
-
我们维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;
-
我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate,随后我们判断 x:
- 如果 x 与 candidate 相等,那么计数器 count 的值增加 1;
- 如果 x 与 candidate 不等,那么计数器 count 的值减少 1。
-
在遍历完成后,candidate 即为整个数组的众数。
合并链表,寻找第k等都适用。
自己定义好一个优先队列后,它内部会自动对插入的元素进行排序。
PriorityQueue<类型> q = new PriorityQueue<>((x,y)->x.val-y.val);
//x-y是升序,y-x相比于一般二叉树的遍历方法,morris遍历能左到O(1)的空间复杂度。
基本思想是使用线索二叉树进行中序遍历。
遍历过程包含三个部分:
1.创建指向中序后驱结点的线索;
2.遍历输出节点;
3.删除线索,恢复树的结构;
1.当前结点的左孩子是否为空,若是则输出当前节点,更新当前结点为当前节点的右孩子;否则进入2。
2.在当前结点的左子树中寻找中序遍历下的前驱节点(左子树中最右结点)
a.若前驱结点的右孩子为空,则将前驱结点的右孩子指向当前结点,当前结点更新为当前结点的左孩子;进入3;
b.若前驱结点的右孩子为当前结点(不为空),将前驱结点的右孩子置NULL,输出当前结点,当前结点更新为当前结点的右孩子,进入3;
3.若当前结点不为空,进入1;否则程序结束;
public static void inOrder(TreeNode root) {
TreeNode cur = root, pre = null;
for (; cur != null;) {
if (cur.left != null) {
pre = cur.left;
// find predecessor
while (pre.right != null && pre.right != cur)
pre = pre.right;
if (pre.right == null) {// create thread
pre.right = cur;
cur = cur.left;
} else {
print(cur);
pre.right = null;
cur = cur.right;
}
} else {
print(cur);
cur = cur.right;
}
}
}以多个点为起点开始广度优先遍历(全部加入到队列中),但是图中的每一个点只被访问一次(需要一个标志位来确保)。
把一个大的问题分成很多小的问题。对每个小问题求得局部最优解,合起来作为大问题的最优解。
前缀和一般用于数组,指的是==前面i个数的总和==。经过计算使得数组中的每个位置的数都是当前数字和前面所有数的和。这样只需要用当前位置减去前一个位置就能得到当前位置数组的值。
最大值:Integer.MAX_VALUE 2^32-1
最小值:Integer.MIN_VALUE -2^32
不能用整数直接判断是否大于最大值或小于最小值。一个整数超出范围后它的值就不做人了。
Character.getNumericValue(c);
map.getOrDefault(i,c);其中i是根据键获取值,如果没有获取到值就会使用c作为键i的默认值
若使用快慢双指针的方法,从相遇点到入环点的距离加上n−1圈的环长,恰好等于从链表头部到入环点的距离。
当发现 slow与 fast相遇时,我们再额外使用一个指针 ptr。起始,它指向链表头部;随后,它和 slow每次向后移动一个位置。最终,它们会在入环点相遇。
可使用双指针的方法,每个指针对应其中一个字符串的字符数组。如果当前两字符相等且当前读取到的“#”数为0,两指针都减一。如果读取到“#”,就让“#”的数量加一。如果读取到普通字符且“#”号数量大于0就让其减一并跳过(退格)这一个字符,否则等于0的话,就在这里等待,让另一个数组也读到相同处境的字符。比较他们是否相等,不相等立刻返回false。如果两数组同时读完而且没有找到不匹配的字符,就说明他们退格后是相等的字符串。
从左往右寻找递减的子序列,找不到从右边开始删除k个数字即可。找到就删除左边大的数字,找到m或k个之后,就在右边删除k-m个数字即可。
为了减少时间复杂度,用一个栈保存结果。每次读取字符串需要判断栈顶的元素是否比它大,如果是的话就需要出栈==适量==大于字符的元素再让该元素入栈。
1.二叉树展开后的顺序就是二叉树先序遍历的顺序,因此可以先对二叉树进行前序遍历,得到一个list,再根据list的顺序进行展开。
1.2可以用一个prev保存当前list中取出结点的前一个结点。此时展开和遍历就可以同时进行,运行速率更快。
2.对每个结点,找到左子树的最右结点,让其的右孩子等于右子树,再对这个结点的右子树进行递归,最后得到结果。
广度优先遍历,但是为了时间更快一些,不使用队列进行广度优先遍历。使用一个pre指针表示当前结点,他要指向cur的某个子节点。当前层数的next全部指完后,如果还有下一层,cur又会变成下一层的第一个结点并继续指。

使用==双指针==的办法,这里思路很重要。仅使用一次循环,让两个指针分别位于数组的两端,先计算出容器的面积,再把数较小的那个指针向中心挪动,最后完成遍历,可得到正确结果。
思想:缩减搜索空间。指针每一次移动,都意味着排除掉了一个柱子。
(左边小于右边的情况下)如果固定左边的柱子,移动右边的柱子,那么水的高度一定不会增加,且宽度一定减少,所以水的面积一定减少。这个时候,左边的柱子和任意一个其他柱子的组合,其实都可以排除了。也就是我们可以排除掉左边的柱子了。